Program for nth Catalan Number
Last Updated :
22 Nov, 2023
Catalan numbers are defined as a mathematical sequence that consists of positive integers, which can be used to find the number of possibilities of various combinations.
The nth term in the sequence denoted Cn, is found in the following formula: 
The first few Catalan numbers for n = 0, 1, 2, 3, … are : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …
Catalan numbers occur in many interesting counting problems like the following.
- Count the number of expressions containing n pairs of parentheses that are correctly matched. For n = 3, possible expressions are ((())), ()(()), ()()(), (())(), (()()).
- Count the number of possible Binary Search Trees with n keys (See this)
- Count the number of full binary trees (A rooted binary tree is full if every vertex has either two children or no children) with n+1 leaves.
- Given a number n, return the number of ways you can draw n chords in a circle with 2 x n points such that no 2 chords intersect.
See this for more applications.
Examples:
Input: n = 6
Output: 132
Input: n = 8
Output: 1430
Program for nth Catalan Number using Recursion:
Catalan numbers satisfy the following recursive formula: 
Step-by-step approach:
- Base condition for the recursive approach, when n <= 1, return 1
- Iterate from i = 0 to i < n
- Make a recursive call catalan(i) and catalan(n – i – 1) and keep adding the product of both into res.
- Return the res.
Following is the implementation of the above recursive formula.
C++
#include <iostream>
using namespace std;
unsigned long int catalan(unsigned int n)
{
if (n <= 1)
return 1;
unsigned long int res = 0;
for (int i = 0; i < n; i++)
res += catalan(i) * catalan(n - i - 1);
return res;
}
int main()
{
for (int i = 0; i < 10; i++)
cout << catalan(i) << " ";
return 0;
}
|
Java
import java.io.*;
class CatalnNumber {
int catalan(int n)
{
int res = 0;
if (n <= 1) {
return 1;
}
for (int i = 0; i < n; i++) {
res += catalan(i) * catalan(n - i - 1);
}
return res;
}
public static void main(String[] args)
{
CatalnNumber cn = new CatalnNumber();
for (int i = 0; i < 10; i++) {
System.out.print(cn.catalan(i) + " ");
}
}
}
|
Python3
def catalan(n):
if n <= 1:
return 1
res = 0
for i in range(n):
res += catalan(i) * catalan(n-i-1)
return res
for i in range(10):
print(catalan(i), end=" ")
|
C#
using System;
class GFG {
static int catalan(int n)
{
int res = 0;
if (n <= 1) {
return 1;
}
for (int i = 0; i < n; i++) {
res += catalan(i) * catalan(n - i - 1);
}
return res;
}
public static void Main()
{
for (int i = 0; i < 10; i++)
Console.Write(catalan(i) + " ");
}
}
|
Javascript
<script>
function catalan(n)
{
if (n <= 1)
return 1;
let res = 0;
for(let i = 0; i < n; i++)
res += catalan(i) *
catalan(n - i - 1);
return res;
}
for (let i = 0; i < 10; i++)
document.write(catalan(i) + " ");
</script>
|
PHP
<?php
function catalan($n)
{
if ($n <= 1)
return 1;
$res = 0;
for($i = 0; $i < $n; $i++)
$res += catalan($i) *
catalan($n - $i - 1);
return $res;
}
for ($i = 0; $i < 10; $i++)
echo catalan($i), " ";
?>
|
Output1 1 2 5 14 42 132 429 1430 4862
Time Complexity: The above implementation is equivalent to nth Catalan number.

The value of nth Catalan number is exponential which makes the time complexity exponential.
Auxiliary Space: O(n)
Program for nth Catalan Number using Dynamic Programming:
We can observe that the above recursive implementation does a lot of repeated work. Since there are overlapping subproblems, we can use dynamic programming for this.
Step-by-step approach:
- Create an array catalan[] for storing ith Catalan number.
- Initialize, catalan[0] and catalan[1] = 1
- Loop through i = 2 to the given Catalan number n.
- Loop through j = 0 to j < i and Keep adding value of catalan[j] * catalan[i – j – 1] into catalan[i].
- Finally, return catalan[n]
Follow the steps below to implement the above approach:
C++
#include <iostream>
using namespace std;
unsigned long int catalanDP(unsigned int n)
{
unsigned long int catalan[n + 1];
catalan[0] = catalan[1] = 1;
for (int i = 2; i <= n; i++) {
catalan[i] = 0;
for (int j = 0; j < i; j++)
catalan[i] += catalan[j] * catalan[i - j - 1];
}
return catalan[n];
}
int main()
{
for (int i = 0; i < 10; i++)
cout << catalanDP(i) << " ";
return 0;
}
|
Java
import java.io.*;
class GFG {
static int catalanDP(int n)
{
int catalan[] = new int[n + 2];
catalan[0] = 1;
catalan[1] = 1;
for (int i = 2; i <= n; i++) {
catalan[i] = 0;
for (int j = 0; j < i; j++) {
catalan[i]
+= catalan[j] * catalan[i - j - 1];
}
}
return catalan[n];
}
public static void main(String[] args)
{
for (int i = 0; i < 10; i++) {
System.out.print(catalanDP(i) + " ");
}
}
}
|
Python3
def catalan(n):
if (n == 0 or n == 1):
return 1
catalan = [0]*(n+1)
catalan[0] = 1
catalan[1] = 1
for i in range(2, n + 1):
for j in range(i):
catalan[i] += catalan[j] * catalan[i-j-1]
return catalan[n]
for i in range(10):
print(catalan(i), end=" ")
|
C#
using System;
class GFG {
static uint catalanDP(uint n)
{
uint[] catalan = new uint[n + 2];
catalan[0] = catalan[1] = 1;
for (uint i = 2; i <= n; i++) {
catalan[i] = 0;
for (uint j = 0; j < i; j++)
catalan[i]
+= catalan[j] * catalan[i - j - 1];
}
return catalan[n];
}
static void Main()
{
for (uint i = 0; i < 10; i++)
Console.Write(catalanDP(i) + " ");
}
}
|
Javascript
<script>
function catalanDP(n)
{
let catalan= [];
catalan[0] = catalan[1] = 1;
for (let i = 2; i <= n; i++)
{
catalan[i] = 0;
for (let j = 0; j < i; j++)
catalan[i] += catalan[j] *
catalan[i - j - 1];
}
return catalan[n];
}
for (let i = 0; i < 10; i++)
document.write(catalanDP(i) + " ");
</script>
|
PHP
<?php
function catalanDP( $n)
{
$catalan= array();
$catalan[0] = $catalan[1] = 1;
for ($i = 2; $i <= $n; $i++)
{
$catalan[$i] = 0;
for ( $j = 0; $j < $i; $j++)
$catalan[$i] += $catalan[$j] *
$catalan[$i - $j - 1];
}
return $catalan[$n];
}
for ($i = 0; $i < 10; $i++)
echo catalanDP($i) , " ";
?>
|
Output1 1 2 5 14 42 132 429 1430 4862
Time Complexity: O(n2)
Auxiliary Space: O(n)
We can also use the below formula to find nth Catalan number in O(n) time.

Here is the proof for the Expression:–

This is the expression for which we are going to see the proof
In the pascal triangle,
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

Pascal’s triangle as binomial coefficients

the formula for a cell of Pascal’s triangle

Pascal’s triangle

.

.

.
Below are the steps for calculating nCr.
- Create a variable to store the answer and change r to n – r if r is greater than n – r because we know that C(n, r) = C(n, n-r) if r > n – r
- Run a loop from 0 to r-1
- In every iteration update ans as (ans*(n-i))/(i+1), where i is the loop counter.
- So the answer will be equal to ((n/1)*((n-1)/2)*…*((n-r+1)/r), which is equal to nCr.
Below are steps to calculate Catalan numbers using the formula: 2nCn/(n+1)
- Calculate 2nCn using the similar steps that we use to calculate nCr
- Return the value 2nCn/ (n + 1)
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
unsigned long int binomialCoeff(unsigned int n,
unsigned int k)
{
unsigned long int res = 1;
if (k > n - k)
k = n - k;
for (int i = 0; i < k; ++i) {
res *= (n - i);
res /= (i + 1);
}
return res;
}
unsigned long int catalan(unsigned int n)
{
unsigned long int c = binomialCoeff(2 * n, n);
return c / (n + 1);
}
int main()
{
for (int i = 0; i < 10; i++)
cout << catalan(i) << " ";
return 0;
}
|
Java
class GFG {
static long binomialCoeff(int n, int k)
{
long res = 1;
if (k > n - k) {
k = n - k;
}
for (int i = 0; i < k; ++i) {
res *= (n - i);
res /= (i + 1);
}
return res;
}
static long catalan(int n)
{
long c = binomialCoeff(2 * n, n);
return c / (n + 1);
}
public static void main(String[] args)
{
for (int i = 0; i < 10; i++) {
System.out.print(catalan(i) + " ");
}
}
}
|
Python3
def binomialCoefficient(n, k):
if (k > n - k):
k = n - k
res = 1
for i in range(k):
res = res * (n - i)
res = res / (i + 1)
return res
def catalan(n):
c = binomialCoefficient(2*n, n)
return c/(n + 1)
for i in range(10):
print(catalan(i), end=" ")
|
C#
using System;
class GFG {
static long binomialCoeff(int n, int k)
{
long res = 1;
if (k > n - k) {
k = n - k;
}
for (int i = 0; i < k; ++i) {
res *= (n - i);
res /= (i + 1);
}
return res;
}
static long catalan(int n)
{
long c = binomialCoeff(2 * n, n);
return c / (n + 1);
}
public static void Main()
{
for (int i = 0; i < 10; i++) {
Console.Write(catalan(i) + " ");
}
}
}
|
Javascript
<script>
function binomialCoeff(n, k)
{
let res = 1;
if (k > n - k)
k = n - k;
for (let i = 0; i < k; ++i)
{
res *= (n - i);
res = Math.floor(res / (i + 1));
}
return res;
}
function catalan(n)
{
c = binomialCoeff(2 * (n), n);
return Math.floor(c / (n + 1));
}
for (let i = 0; i < 10; i++)
document.write(catalan(i) + " " );
</script>
|
PHP
<?php
function binomialCoeff($n, $k)
{
$res = 1;
if ($k > $n - $k)
$k = $n - $k;
for ($i = 0; $i < $k; ++$i)
{
$res *= ($n - $i);
$res = floor($res / ($i + 1));
}
return $res;
}
function catalan($n)
{
$c = binomialCoeff(2 * ($n), $n);
return floor($c / ($n + 1));
}
for ($i = 0; $i < 10; $i++)
echo catalan($i), " " ;
?>
|
Output1 1 2 5 14 42 132 429 1430 4862
Time Complexity: O(n).
Auxiliary Space: O(1)
We can also use the below formulas to find nth Catalan number in O(n) time.


Program for nth Catalan Number using the (n-1)th Catalan Number:
We already know how to calculate the nth Catalan Number using the below formula, 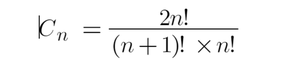
This formula can be further simplified to express the nth Catalan Number in the terms of (n-1)th Catalan Number,
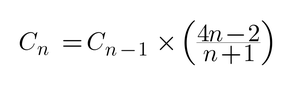
Below are steps to calculate Catalan numbers using the above formula:
- Initialize a variable res = 1
- Print 1 as the first Catalan Number
- Iterate from i = 1 to i < n
- Update res with res = (res * (4 * i – 2)) / (i + 1)
- print res
Below is the implementation for the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void catalan(int n)
{
int res = 1;
cout << res << " ";
for (int i = 1; i < n; i++) {
res = (res * (4 * i - 2)) / (i + 1);
cout << res << " ";
}
}
int main()
{
int n = 10;
catalan(n);
return 0;
}
|
Java
import java.util.*;
class GFG {
static void catalan(int n)
{
int res = 1;
System.out.print(1 + " ");
for (int i = 1; i < n; i++) {
res = (res * (4 * i - 2)) / (i + 1);
System.out.print(res + " ");
}
}
public static void main(String args[])
{
int n = 10;
catalan(n);
}
}
|
Python3
def catalan(n):
res = 1
print(1, end=" ")
for i in range(1, n):
res = (res * (4 * i - 2)) // (i + 1)
print(res, end=" ")
n = 10
catalan(n)
|
C#
using System;
public class GFG {
static void catalan(int n)
{
int res = 1;
Console.Write(1 + " ");
for (int i = 1; i < n; i++) {
res = (res * (4 * i - 2)) / (i + 1);
Console.Write(res + " ");
}
}
public static void Main(String[] args)
{
int n = 10;
catalan(n);
}
}
|
Javascript
<script>
function catalan(n)
{
let res = 1;
document.write(1 + " ");
for (let i = 1; i < n; i++)
{
res = (res * (4 * i - 2)) / (i + 1);
document.write(res + " ");
}
}
let n = 10;
catalan(n);
</script>
|
Output1 1 2 5 14 42 132 429 1430 4862
Time Complexity: O(n)
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...