Number of Triangles in an Undirected Graph

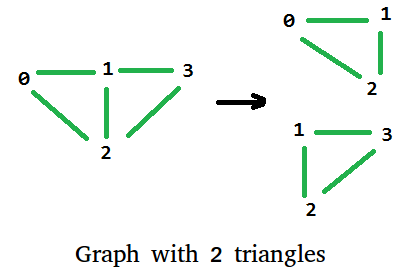
Given an Undirected simple graph, We need to find how many triangles it can have. For example below graph have 2 triangles in it.

Let A[][] be the adjacency matrix representation of the graph. If we calculate A³, then the number of triangles in Undirected Graph is equal to trace(A³) / 6. Where trace(A) is the sum of the elements on the main diagonal of matrix A. 

Trace of a graph represented as adjacency matrix A[V][V] is,
trace(A[V][V]) = A[0][0] + A[1][1] + .... + A[V-1][V-1]

Count of triangles = trace(A3) / 6

Below is the implementation of the above formula. 

C++

// A C++ program for finding
// number of triangles in an
// Undirected Graph. The program
// is for adjacency matrix
// representation of the graph
#include <bits/stdc++.h>
using namespace std;

// Number of vertices in the graph
#define V 4

//  Utility function for matrix
// multiplication
void multiply(int A[][V], int B[][V], int C[][V])
{
    for (int i = 0; i < V; i++)
    {
        for (int j = 0; j < V; j++)
        {
            C[i][j] = 0;
            for (int k = 0; k < V; k++)
                C[i][j] += A[i][k]*B[k][j];
        }
    }
}

// Utility function to calculate
// trace of a matrix (sum of
// diagonal elements)
int getTrace(int graph[][V])
{
    int trace = 0;
    for (int i = 0; i < V; i++)
        trace += graph[i][i];
    return trace;
}

//  Utility function for calculating
// number of triangles in graph
int triangleInGraph(int graph[][V])
{
    // To Store graph^2
    int aux2[V][V];

    // To Store graph^3
    int aux3[V][V];

    //  Initialising aux
    // matrices with 0
    for (int i = 0; i < V; ++i)
        for (int j = 0; j < V; ++j)
            aux2[i][j] = aux3[i][j] = 0;

    // aux2 is graph^2 now  printMatrix(aux2);
    multiply(graph, graph, aux2);

    // after this multiplication aux3 is
    // graph^3 printMatrix(aux3);
    multiply(graph, aux2, aux3);

    int trace = getTrace(aux3);
    return trace / 6;
}

// driver code
int main()
{

    int graph[V][V] = {{0, 1, 1, 0},
                       {1, 0, 1, 1},
                       {1, 1, 0, 1},
                       {0, 1, 1, 0}
                      };

    printf("Total number of Triangle in Graph : %d\n",
            triangleInGraph(graph));
    return 0;
}

Java

// Java program to find number
// of triangles in an Undirected
// Graph. The program is for
// adjacency matrix representation
// of the graph
import java.io.*;

class Directed
{
    // Number of vertices in
    // the graph
    int V = 4;

   //  Utility function for
   // matrix multiplication
   void multiply(int A[][], int B[][],
                            int C[][])
   {
       for (int i = 0; i < V; i++)
       {
           for (int j = 0; j < V; j++)
           {
               C[i][j] = 0;
               for (int k = 0; k < V;
                                   k++)
               {
                   C[i][j] += A[i][k]*
                              B[k][j];
               }
           }
       }
   }

   // Utility function to calculate
   // trace of a matrix (sum of
   // diagonal elements)
   int getTrace(int graph[][])
   {
       int trace = 0;

       for (int i = 0; i < V; i++)
       {
           trace += graph[i][i];
       }
       return trace;
   }

   // Utility function for
   // calculating number of
   // triangles in graph
   int triangleInGraph(int graph[][])
   {
       // To Store graph^2
       int[][] aux2 = new int[V][V];

       // To Store graph^3
       int[][] aux3 = new int[V][V];

       // Initialising aux matrices
       // with 0
       for (int i = 0; i < V; ++i)
       {
           for (int j = 0; j < V; ++j)
           {
               aux2[i][j] = aux3[i][j] = 0;
           }
       }

       // aux2 is graph^2 now
       // printMatrix(aux2)
       multiply(graph, graph, aux2);

       // after this multiplication aux3
       // is graph^3 printMatrix(aux3)
       multiply(graph, aux2, aux3);

       int trace = getTrace(aux3);

       return trace / 6;
   }

   // Driver code
   public static void main(String args[])
   {
       Directed obj = new Directed();

       int graph[][] = { {0, 1, 1, 0},
                         {1, 0, 1, 1},
                         {1, 1, 0, 1},
                         {0, 1, 1, 0}
                       };

       System.out.println("Total number of Triangle in Graph : "+
              obj.triangleInGraph(graph));
   }
}

// This code is contributed by Anshika Goyal.

Python3

# A Python3 program for finding number of
# triangles in an Undirected Graph. The
# program is for adjacency matrix
# representation of the graph

# Utility function for matrix
# multiplication
def multiply(A, B, C):
    global V
    for i in range(V):
        for j in range(V):
            C[i][j] = 0
            for k in range(V):
                C[i][j] += A[i][k] * B[k][j]

# Utility function to calculate
# trace of a matrix (sum of
# diagonal elements)
def getTrace(graph):
    global V
    trace = 0
    for i in range(V):
        trace += graph[i][i]
    return trace

# Utility function for calculating
# number of triangles in graph
def triangleInGraph(graph):
    global V

    # To Store graph^2
    aux2 = [[None] * V for i in range(V)]

    # To Store graph^3
    aux3 = [[None] * V for i in range(V)]

    # Initialising aux
    # matrices with 0
    for i in range(V):
        for j in range(V):
            aux2[i][j] = aux3[i][j] = 0

    # aux2 is graph^2 now printMatrix(aux2)
    multiply(graph, graph, aux2)

    # after this multiplication aux3 is
    # graph^3 printMatrix(aux3)
    multiply(graph, aux2, aux3)

    trace = getTrace(aux3)
    return trace // 6

# Driver Code

# Number of vertices in the graph
V = 4
graph = [[0, 1, 1, 0],
         [1, 0, 1, 1],
         [1, 1, 0, 1],
         [0, 1, 1, 0]]

print("Total number of Triangle in Graph :",
                    triangleInGraph(graph))

# This code is contributed by PranchalK

C#

// C# program to find number
// of triangles in an Undirected
// Graph. The program is for
// adjacency matrix representation
// of the graph
using System;

class GFG
{
// Number of vertices
// in the graph
int V = 4;

// Utility function for
// matrix multiplication
void multiply(int [,]A, int [,]B,
                        int [,]C)
{
    for (int i = 0; i < V; i++)
    {
        for (int j = 0; j < V; j++)
        {
            C[i, j] = 0;
            for (int k = 0; k < V;
                              k++)
            {
                C[i, j] += A[i, k]*
                           B[k, j];
            }
        }
    }
}

// Utility function to
// calculate trace of
// a matrix (sum of
// diagonal elements)
int getTrace(int [,]graph)
{
    int trace = 0;

    for (int i = 0; i < V; i++)
    {
        trace += graph[i, i];
    }
    return trace;
}

// Utility function for
// calculating number of
// triangles in graph
int triangleInGraph(int [,]graph)
{
    // To Store graph^2
    int[,] aux2 = new int[V, V];

    // To Store graph^3
    int[,] aux3 = new int[V, V];

    // Initialising aux matrices
    // with 0
    for (int i = 0; i < V; ++i)
    {
        for (int j = 0; j < V; ++j)
        {
            aux2[i, j] = aux3[i, j] = 0;
        }
    }

    // aux2 is graph^2 now
    // printMatrix(aux2)
    multiply(graph, graph, aux2);

    // after this multiplication aux3
    // is graph^3 printMatrix(aux3)
    multiply(graph, aux2, aux3);

    int trace = getTrace(aux3);

    return trace / 6;
}

// Driver code
public static void Main()
{
    GFG obj = new GFG();

    int [,]graph = {{0, 1, 1, 0},
                    {1, 0, 1, 1},
                    {1, 1, 0, 1},
                    {0, 1, 1, 0}};

    Console.WriteLine("Total number of " +
                   "Triangle in Graph : "+
              obj.triangleInGraph(graph));
}
}

// This code is contributed by anuj_67.

Javascript

<script>

// Javascript program to find number
// of triangles in an Undirected
// Graph. The program is for
// adjacency matrix representation
// of the graph

// Number of vertices in the graph
let V = 4;

//  Utility function for matrix
// multiplication
function multiply(A, B, C)
{
    for(let i = 0; i < V; i++)
    {
        for(let j = 0; j < V; j++)
        {
            C[i][j] = 0;
            for(let k = 0; k < V; k++)
                C[i][j] += A[i][k] * B[k][j];
        }
    }
}

// Utility function to calculate
// trace of a matrix (sum of
// diagonal elements)
function getTrace(graph)
{
    let trace = 0;
    for(let i = 0; i < V; i++)
        trace += graph[i][i];

    return trace;
}

//  Utility function for calculating
// number of triangles in graph
function triangleInGraph(graph)
{

    // To Store graph^2
    let aux2 = new Array(V);

    // To Store graph^3
    let aux3 = new Array(V);

    // Initialising aux
    // matrices with 0
    for(let i = 0; i < V; ++i)
    {
        aux2[i] = new Array(V);
        aux3[i] = new Array(V);
        for(let j = 0; j < V; ++j)
        {
            aux2[i][j] = aux3[i][j] = 0;
        }
    }

    // aux2 is graph^2 now  printMatrix(aux2);
    multiply(graph, graph, aux2);

    // After this multiplication aux3 is
    // graph^3 printMatrix(aux3);
    multiply(graph, aux2, aux3);

    let trace = getTrace(aux3);
    return (trace / 6);
}

// Driver code
let graph = [ [ 0, 1, 1, 0 ],
              [ 1, 0, 1, 1 ],
              [ 1, 1, 0, 1 ],
              [ 0, 1, 1, 0 ] ];

document.write("Total number of Triangle in Graph : " +
               triangleInGraph(graph));

// This code is contributed by divyesh072019

</script>

Output

Total number of Triangle in Graph : 2

How does this work?
If we compute Aⁿ for an adjacency matrix representation of the graph, then a value Aⁿ[i][j] represents the number of distinct walks between vertex i to j in the graph. In A³, we get all distinct paths of length 3 between every pair of vertices.
A triangle is a cyclic path of length three, i.e. begins and ends at the same vertex. So A³[i][i] represents a triangle beginning and ending with vertex i. Since a triangle has three vertices and it is counted for every vertex, we need to divide the result by 3. Furthermore, since the graph is undirected, every triangle twice as i-p-q-j and i-q-p-j, so we divide by 2 also. Therefore, the number of triangles is trace(A³) / 6.

Time Complexity: O(V3) (as here most time consuming part is multiplication of matrix which contains 3 nested for loops)
Space Complexity: O(V2) (to store matrix of size V*V)

Time Complexity: 
The time complexity of above algorithm is O(V³) where V is number of vertices in the graph, we can improve the performance to O(V^2.8074) using Strassen’s matrix multiplication algorithm.

Another approach: Using Bitsets as adjacency lists.

• For each node in the graph compute the corresponding adjacency list as a bitmask.
• If two nodes, i & j, are adjacent compute the number of nodes that are adjacent to i & j and add it to the answer.
• In the end, divide the answer by 6 to avoid duplicates.

In order to compute the number of nodes adjacent to two nodes, i & j, we use the bitwise operation & (and) on the adjacency list of i and j, then we count the number of ones.

Below is the implementation of the above approach:

C++

#include<iostream>
#include<string>
#include<algorithm>
#include<cstring>
#include<vector>
#include<bitset>

using namespace std;

#define V 4

int main()
{
    // Graph represented as adjacency matrix
    int graph[][V] = {{0, 1, 1, 0},
                      {1, 0, 1, 1},
                      {1, 1, 0, 1},
                      {0, 1, 1, 0}};

    // create the adjacency list of the graph (as bit masks)
    // set the bits at positions [i][j] & [j][i] to 1, if there is an undirected edge between i and j
    vector<bitset<V>> Bitset_Adj_List(V);
    for (int i = 0; i < V;i++)
        for (int j = 0; j < V;j++)
            if(graph[i][j])
                Bitset_Adj_List[i][j] = 1,
                Bitset_Adj_List[j][i] = 1;

    int ans = 0;

    for (int i = 0; i < V;i++)
        for (int j = 0; j < V;j++)

            // if i & j are adjacent
            // compute the number of nodes that are adjacent to i & j
            if(Bitset_Adj_List[i][j] == 1 && i != j){
                bitset<V> Mask = Bitset_Adj_List[i] & Bitset_Adj_List[j];
                ans += Mask.count();
            }

   // divide the answer by 6 to avoid duplicates
   ans /= 6;

   cout << "The number of Triangles in the Graph is : " << ans;

    // This code is contributed
    // by Gatea David
}

Java

import java.util.*;

public class Main
{
    static final int V = 4;

    public static void main(String[] args) {

        // Graph represented as adjacency matrix
        int graph[][] = {{0, 1, 1, 0},
                    {1, 0, 1, 1},
                    {1, 1, 0, 1},
                    {0, 1, 1, 0}};

        // create the adjacency list of the graph (as bit masks)
       // set the bits at positions [i][j] & [j][i] to 1,
      // if there is an undirected edge between i and j
        Vector<BitSet> Bitset_Adj_List = new Vector<BitSet>();
        for(int i=0; i<V; i++)
        {
            Bitset_Adj_List.add(new BitSet());
            for(int j=0; j<V; j++)
            {
                if(graph[i][j] == 1)
                Bitset_Adj_List.get(i).set(j, true);
            }
        }

        int ans = 0;

        for(int i=0; i<V; i++)
            for(int j=0; j<V; j++)

        // if i & j are adjacent
        // compute the number of nodes that are adjacent to i & j
        if(Bitset_Adj_List.get(i).get(j) == true && i!=j)
        {
            BitSet Mask = (BitSet) Bitset_Adj_List.get(i).clone();
            Mask.and(Bitset_Adj_List.get(j));
            ans += Mask.cardinality();
        }

       // divide the answer by 6 to avoid duplicates
       ans /= 6;

       System.out.println("The number of Triangles in the Graph is : " + ans);

    }
}

Javascript

function main() {
const V = 4;

  // Graph represented as adjacency matrix
  let graph = [[0, 1, 1, 0],
              [1, 0, 1, 1],
              [1, 1, 0, 1],
              [0, 1, 1, 0]];

  // create the adjacency list of the graph (as bit masks)
  let Bitset_Adj_List = [];
  for(let i=0; i<V; i++) {
    Bitset_Adj_List[i] = new Array(V).fill(0);
    for(let j=0; j<V; j++) {
      if(graph[i][j] == 1) {
        Bitset_Adj_List[i][j] = 1;
      }
    }
  }

  let ans = 0;

  for(let i=0; i<V; i++) {
    for(let j=0; j<V; j++) {
      // if i & j are adjacent
      // compute the number of nodes that are adjacent to i & j
      if(Bitset_Adj_List[i][j] == 1 && i!=j) {
        let Mask = Bitset_Adj_List[i].slice();
        for(let k = 0; k < Mask.length; k++) {
          Mask[k] = Mask[k] & Bitset_Adj_List[j][k];
        }
        ans += Mask.filter(i => i==1).length;
      }
    }
  }

  // divide the answer by 6 to avoid duplicates
  ans /= 6;

  console.log("The number of Triangles in the Graph is : " + ans);
}

main();
// this code is contributed by devendra

Python3

# Python3 Program to count number of
# triangles in a Graph

V = 4

# Adjacency Matrix
Graph = [[0, 1, 1, 0],
         [1, 0, 1, 1],
         [1, 1, 0, 1],
         [0, 1, 1, 0 ]]

# Function to find the number of
# triangles in a graph
def findNumberOfTriangles(graph):
    count = 0
    n = len(graph)
    for i in range(n):
        for j in range(n):
            if(graph[i][j] == 1):
                for k in range(n):
                    if(graph[j][k] == 1 and graph[k][i] == 1):
                        count += 1

    return count // 6

# Driver Code
ans = findNumberOfTriangles(Graph)
print("The number of Triangles in the Graph is : ", ans)

C#

using System;
using System.Collections;

class MainClass {
    static int V = 4;

    public static void Main() {

        // Graph represented as adjacency matrix
        int[,] graph = {{0, 1, 1, 0},
                        {1, 0, 1, 1},
                        {1, 1, 0, 1},
                        {0, 1, 1, 0}};

        // create the adjacency list of the graph (as bit masks)
        // set the bits at positions [i,j] & [j,i] to 1,
        // if there is an undirected edge between i and j
        ArrayList Bitset_Adj_List = new ArrayList();
        for(int i=0; i<V; i++) {
            Bitset_Adj_List.Add(new BitArray(V));
            for(int j=0; j<V; j++) {
                if(graph[i,j] == 1)
                    ((BitArray)Bitset_Adj_List[i]).Set(j, true);
            }
        }

        int ans = 0;

        for(int i=0; i<V; i++) {
            for(int j=0; j<V; j++) {

                // if i & j are adjacent
                // compute the number of nodes that are adjacent to i & j
                if(((BitArray)Bitset_Adj_List[i])[j] == true && i!=j) {
                    BitArray Mask = (BitArray)((BitArray)Bitset_Adj_List[i]).Clone();
                    Mask.And(Bitset_Adj_List[j] as BitArray);

                    int count = 0;
                    for(int k = 0; k < V; k++) {
                        if(Mask[k])
                            count++;
                    }

                    ans += count;
                }
            }
        }

        // divide the answer by 6 to avoid duplicates
        ans /= 6;

        Console.WriteLine("The number of Triangles in the Graph is : " + ans);
    }
}

Output

The number of Triangles in the Graph is : 2

Time Complexity: First we have the two for nested loops O(V²) flowed by Bitset operations & and count, both have a time complexity of O(V / Word RAM), where V = number of nodes in the graph and Word RAM is usually 32 or 64. So the final time complexity is O(V² * V / 32) or O(V³).

Time Complexity: O(V3)
Space Complexity: O(V2)

References:

http://www.d.umn.edu/math/Technical%20Reports/Technical%20Reports%202007-/TR%202012/yang.pdf

Number of Triangles in Directed and Undirected Graphs. 

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.