A board of length m and width n is given, we need to break this board into m*n squares such that cost of breaking is minimum. cutting cost for each edge will be given for the board. In short, we need to choose such a sequence of cutting such that cost is minimized.
Examples:
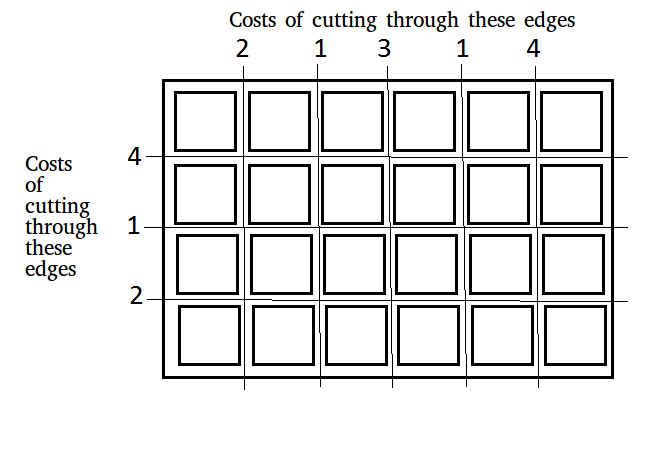
For above board optimal way to cut into square is:
Total minimum cost in above case is 42. It is
evaluated using following steps.
Initial Value : Total_cost = 0
Total_cost = Total_cost + edge_cost * total_pieces
Cost 4 Horizontal cut Cost = 0 + 4*1 = 4
Cost 4 Vertical cut Cost = 4 + 4*2 = 12
Cost 3 Vertical cut Cost = 12 + 3*2 = 18
Cost 2 Horizontal cut Cost = 18 + 2*3 = 24
Cost 2 Vertical cut Cost = 24 + 2*3 = 30
Cost 1 Horizontal cut Cost = 30 + 1*4 = 34
Cost 1 Vertical cut Cost = 34 + 1*4 = 38
Cost 1 Vertical cut Cost = 38 + 1*4 = 42
Minimum Cost to cut a board into squares using a greedy algorithm:
This problem can be solved by greedy approach . To get minimum cost , the idea is to cut the edge with highest cost first because we have less number of pieces and after every cut the number of pieces increase . As the question stated Total_cost = Total_cost + edge_cost * total_pieces .
- At first sort both the array in non-ascending order
- We keep count of two variables vert(keeps track of vertical pieces) and hzntl(keeps track of horizontal pieces). We will initialize both of them with 1.
- We will keep track of two pointers starting from 0th index of both the array
- Now we will take the highest cost edge from those pointers and multiply them with the corresponding variable. That is if we cut a horizontal cut we will add (edge_cost*hzntl) and increase vert by 1 and if we cut a vertical cut we will add(edge_cost*vert) and increase hzntl bt 1 .
- After cutting all the edges we will get the minimum cost
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumCostOfBreaking(int X[], int Y[], int m, int n)
{
int res = 0;
sort(X, X + m, greater<int>());
sort(Y, Y + n, greater<int>());
int hzntl = 1, vert = 1;
int i = 0, j = 0;
while (i < m && j < n)
{
if (X[i] > Y[j])
{
res += X[i] * vert;
hzntl++;
i++;
}
else
{
res += Y[j] * hzntl;
vert++;
j++;
}
}
int total = 0;
while (i < m)
total += X[i++];
res += total * vert;
total = 0;
while (j < n)
total += Y[j++];
res += total * hzntl;
return res;
}
int main()
{
int m = 6, n = 4;
int X[m-1] = {2, 1, 3, 1, 4};
int Y[n-1] = {4, 1, 2};
cout << minimumCostOfBreaking(X, Y, m-1, n-1);
return 0;
}
|
Java
import java.util.Arrays;
import java.util.Collections;
class GFG
{
static int minimumCostOfBreaking(Integer X[], Integer Y[],
int m, int n)
{
int res = 0;
Arrays.sort(X, Collections.reverseOrder());
Arrays.sort(Y, Collections.reverseOrder());
int hzntl = 1, vert = 1;
int i = 0, j = 0;
while (i < m && j < n)
{
if (X[i] > Y[j])
{
res += X[i] * vert;
hzntl++;
i++;
}
else
{
res += Y[j] * hzntl;
vert++;
j++;
}
}
int total = 0;
while (i < m)
total += X[i++];
res += total * vert;
total = 0;
while (j < n)
total += Y[j++];
res += total * hzntl;
return res;
}
public static void main(String arg[])
{
int m = 6, n = 4;
Integer X[] = {2, 1, 3, 1, 4};
Integer Y[] = {4, 1, 2};
System.out.print(minimumCostOfBreaking(X, Y, m-1, n-1));
}
}
|
Python3
def minimumCostOfBreaking(X, Y, m, n):
res = 0
X.sort(reverse = True)
Y.sort(reverse = True)
hzntl = 1; vert = 1
i = 0; j = 0
while (i < m and j < n):
if (X[i] > Y[j]):
res += X[i] * vert
hzntl += 1
i += 1
else:
res += Y[j] * hzntl
vert += 1
j += 1
total = 0
while (i < m):
total += X[i]
i += 1
res += total * vert
total = 0
while (j < n):
total += Y[j]
j += 1
res += total * hzntl
return res
m = 6; n = 4
X = [2, 1, 3, 1, 4]
Y = [4, 1, 2]
print(minimumCostOfBreaking(X, Y, m-1, n-1))
|
C#
using System;
class GFG
{
static int minimumCostOfBreaking(int[] X, int[] Y,
int m, int n)
{
int res = 0;
Array.Sort<int>(X, new Comparison<int>(
(i1, i2) => i2.CompareTo(i1)));
Array.Sort<int>(Y, new Comparison<int>(
(i1, i2) => i2.CompareTo(i1)));
int hzntl = 1, vert = 1;
int i = 0, j = 0;
while (i < m && j < n)
{
if (X[i] > Y[j])
{
res += X[i] * vert;
hzntl++;
i++;
}
else
{
res += Y[j] * hzntl;
vert++;
j++;
}
}
int total = 0;
while (i < m)
total += X[i++];
res += total * vert;
total = 0;
while (j < n)
total += Y[j++];
res += total * hzntl;
return res;
}
public static void Main(String []arg)
{
int m = 6, n = 4;
int []X = {2, 1, 3, 1, 4};
int []Y = {4, 1, 2};
Console.WriteLine(minimumCostOfBreaking(X, Y, m-1, n-1));
}
}
|
Javascript
<script>
function minimumCostOfBreaking(X, Y, m, n)
{
let res = 0;
X.sort();
X.reverse();
Y.sort();
Y.reverse();
let hzntl = 1, vert = 1;
let i = 0, j = 0;
while (i < m && j < n)
{
if (X[i] > Y[j])
{
res += X[i] * vert;
hzntl++;
i++;
}
else
{
res += Y[j] * hzntl;
vert++;
j++;
}
}
let total = 0;
while (i < m)
total += X[i++];
res += total * vert;
total = 0;
while (j < n)
total += Y[j++];
res += total * hzntl;
return res;
}
let m = 6, n = 4;
let X = [2, 1, 3, 1, 4];
let Y = [4, 1, 2];
document.write(minimumCostOfBreaking(X, Y, m-1, n-1));
</script>
|
Time Complexity: O(mlogm + nlogn), where n and m are the sizes of the given arrays.
Auxiliary Space: O(1)
This article is contributed by Utkarsh Trivedi. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.