Merge two sorted linked lists
Last Updated :
04 Mar, 2024
Given two sorted linked lists consisting of N and M nodes respectively. The task is to merge both of the lists (in place) and return the head of the merged list.
Examples:
Input: a: 5->10->15, b: 2->3->20
Output: 2->3->5->10->15->20
Input: a: 1->1, b: 2->4
Output: 1->1->2->4
Brute Force Way:
The Approach:
In this Approach we use a vector of (n+m) size where n and m are length respective linked list and then store all the element in vector and then we sort the vector and make new linked list it will be our answer.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node* next;
};
Node* newNode(int key){
Node* temp = new Node;
temp->key = key;
temp->next = NULL;
return temp;
}
int main() {
Node* a = newNode(5);
a->next = newNode(10);
a->next->next = newNode(15);
a->next->next->next = newNode(40);
Node* b = newNode(2);
b->next = newNode(3);
b->next->next = newNode(20);
vector<int>v;
while(a!=NULL){
v.push_back(a->key);
a=a->next;
}
while(b!=NULL){
v.push_back(b->key);
b=b->next;
}
sort(v.begin(),v.end());
Node* result= newNode(-1);
Node* temp=result;
for(int i=0;i<v.size();i++){
result->next=newNode(v[i]);
result=result->next;
}
temp=temp->next;
cout<<"Resultant Merge Linked List Is :"<<endl;
while(temp!=NULL){
cout<<temp->key<<" ";
temp=temp->next;
}
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
class Node {
int key;
Node next;
public Node(int key) {
this.key = key;
next = null;
}
}
public class Main {
public static Node newNode(int key) {
return new Node(key);
}
public static void main(String[] args) {
Node a = new Node(5);
a.next = new Node(10);
a.next.next = new Node(15);
a.next.next.next = new Node(40);
Node b = new Node(2);
b.next = new Node(3);
b.next.next = new Node(20);
List<Integer> v = new ArrayList<>();
while (a != null) {
v.add(a.key);
a = a.next;
}
while (b != null) {
v.add(b.key);
b = b.next;
}
Collections.sort(v);
Node result = new Node(-1);
Node temp = result;
for (int i = 0; i < v.size(); i++) {
result.next = new Node(v.get(i));
result = result.next;
}
temp = temp.next;
System.out.print("Resultant Merge Linked List is : ");
while (temp != null) {
System.out.print(temp.key + " ");
temp = temp.next;
}
}
}
|
C#
using System;
using System.Collections.Generic;
using System.Collections;
using System.Linq;
public class Node {
public int key;
public Node next;
public Node(int d)
{
key = d;
next = null;
}
}
class GFG : IComparer<int>
{
public int Compare(int x, int y)
{
if (x == 0 || y == 0)
{
return 0;
}
return x.CompareTo(y);
}
}
class HelloWorld {
public static Node newNode(int key){
Node temp = new Node(key);
temp.next = null;
return temp;
}
static void Main() {
Node a = newNode(5);
a.next = newNode(10);
a.next.next = newNode(15);
a.next.next.next = newNode(40);
Node b = newNode(2);
b.next = newNode(3);
b.next.next = newNode(20);
List<int> v = new List<int>();
while(a!=null){
v.Add(a.key);
a=a.next;
}
while(b!=null){
v.Add(b.key);
b=b.next;
}
GFG gg = new GFG();
v.Sort(gg);
Node result= newNode(-1);
Node temp=result;
for(int i=0;i<v.Count;i++){
result.next=newNode(v[i]);
result=result.next;
}
temp=temp.next;
Console.WriteLine("Resultant Merge Linked List Is :");
while(temp!=null){
Console.Write(temp.key + " ");
temp=temp.next;
}
}
}
|
Javascript
class Node{
constructor(key){
this.key = key;
this.next = null;
}
}
function newNode(key){
let temp = new Node(key);
return temp;
}
let a = newNode(5);
a.next = newNode(10);
a.next.next = newNode(15);
a.next.next.next = newNode(40);
let b = newNode(2);
b.next = newNode(3);
b.next.next = newNode(20);
let v = [];
while(a != null){
v.push(a.key);
a = a.next;
}
while(b != null){
v.push(b.key);
b = b.next;
}
v.sort(function(a, b){return a - b});
let result = newNode(-1);
let temp = result;
for(let i = 0; i<v.length; i++){
result.next = newNode(v[i]);
result = result.next;
}
temp = temp.next;
console.log("Resultant Merge Linked List is : ");
while(temp != null){
console.log(temp.key + " ");
temp = temp.next;
}
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.next = None
def newNode(key):
return Node(key)
a = Node(5)
a.next = Node(10)
a.next.next = Node(15)
a.next.next.next = Node(40)
b = Node(2)
b.next = Node(3)
b.next.next = Node(20)
v = []
while(a is not None):
v.append(a.key)
a = a.next
while(b is not None):
v.append(b.key)
b = b.next
v.sort()
result = Node(-1)
temp = result
for i in range(len(v)):
result.next = Node(v[i])
result = result.next
temp = temp.next
print("Resultant Merge Linked List is : ")
while(temp is not None):
print(temp.key, end=" ")
temp = temp.next
|
Output
Resultant Merge Linked List Is :
2 3 5 10 15 20 40
Time Complexity:O((n+m)+(n+m)*log(n+m)),(n+m)for traversing linked lists and (n+m)*log(n+m) for sorting vector which can be further solved to O((n+m)*log(n+m)).
Auxiliary Space: O(n+m), for vector.
Merge two sorted linked lists using Dummy Nodes:
The idea is to use a temporary dummy node as the start of the result list. The pointer Tail always points to the last node in the result list, so appending new nodes is easy.
Follow the below illustration for a better understanding:
Illustration:
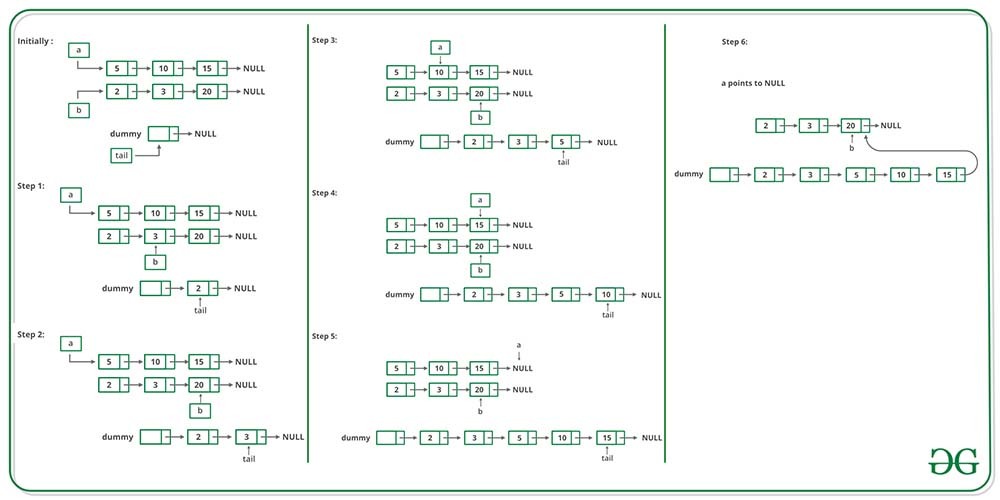
Follow the steps below to solve the problem:
- First, make a dummy node for the new merged linked list
- Now make two pointers, one will point to list1 and another will point to list2.
- Now traverse the lists till one of them gets exhausted.
- If the value of the node pointing to either list is smaller than another pointer, add that node to our merged list and increment that pointer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
};
void MoveNode(Node** destRef, Node** sourceRef);
Node* SortedMerge(Node* a, Node* b)
{
Node dummy;
Node* tail = &dummy;
dummy.next = NULL;
while (1) {
if (a == NULL) {
tail->next = b;
break;
}
else if (b == NULL) {
tail->next = a;
break;
}
if (a->data <= b->data)
MoveNode(&(tail->next), &a);
else
MoveNode(&(tail->next), &b);
tail = tail->next;
}
return (dummy.next);
}
void MoveNode(Node** destRef, Node** sourceRef)
{
Node* newNode = *sourceRef;
assert(newNode != NULL);
*sourceRef = newNode->next;
newNode->next = *destRef;
*destRef = newNode;
}
void push(Node** head_ref, int new_data)
{
Node* new_node = new Node();
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void printList(Node* node)
{
while (node != NULL) {
cout << node->data << " ";
node = node->next;
}
}
int main()
{
Node* res = NULL;
Node* a = NULL;
Node* b = NULL;
push(&a, 15);
push(&a, 10);
push(&a, 5);
push(&b, 20);
push(&b, 3);
push(&b, 2);
res = SortedMerge(a, b);
cout << "Merged Linked List is: \n";
printList(res);
return 0;
}
|
C
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
void MoveNode(struct Node** destRef,
struct Node** sourceRef);
struct Node* SortedMerge(struct Node* a, struct Node* b)
{
struct Node dummy;
struct Node* tail = &dummy;
dummy.next = NULL;
while (1) {
if (a == NULL) {
tail->next = b;
break;
}
else if (b == NULL) {
tail->next = a;
break;
}
if (a->data <= b->data)
MoveNode(&(tail->next), &a);
else
MoveNode(&(tail->next), &b);
tail = tail->next;
}
return (dummy.next);
}
void MoveNode(struct Node** destRef,
struct Node** sourceRef)
{
struct Node* newNode = *sourceRef;
assert(newNode != NULL);
*sourceRef = newNode->next;
newNode->next = *destRef;
*destRef = newNode;
}
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node
= (struct Node*)malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void printList(struct Node* node)
{
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
int main()
{
struct Node* res = NULL;
struct Node* a = NULL;
struct Node* b = NULL;
push(&a, 15);
push(&a, 10);
push(&a, 5);
push(&b, 20);
push(&b, 3);
push(&b, 2);
res = SortedMerge(a, b);
printf("Merged Linked List is: \n");
printList(res);
return 0;
}
|
Java
import java.util.*;
class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
class MergeLists {
Node head;
public void addToTheLast(Node node)
{
if (head == null) {
head = node;
}
else {
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = node;
}
}
void printList()
{
Node temp = head;
while (temp != null) {
System.out.print(temp.data + " ");
temp = temp.next;
}
System.out.println();
}
public static void main(String args[])
{
MergeLists llist1 = new MergeLists();
MergeLists llist2 = new MergeLists();
llist1.addToTheLast(new Node(5));
llist1.addToTheLast(new Node(10));
llist1.addToTheLast(new Node(15));
llist2.addToTheLast(new Node(2));
llist2.addToTheLast(new Node(3));
llist2.addToTheLast(new Node(20));
llist1.head = new Gfg().sortedMerge(llist1.head,
llist2.head);
System.out.println("Merged Linked List is:");
llist1.printList();
}
}
class Gfg {
Node sortedMerge(Node headA, Node headB)
{
Node dummyNode = new Node(0);
Node tail = dummyNode;
while (true) {
if (headA == null) {
tail.next = headB;
break;
}
if (headB == null) {
tail.next = headA;
break;
}
if (headA.data <= headB.data) {
tail.next = headA;
headA = headA.next;
}
else {
tail.next = headB;
headB = headB.next;
}
tail = tail.next;
}
return dummyNode.next;
}
}
|
C#
using System;
public class Node {
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
}
}
public class MergeLists {
Node head;
public void addToTheLast(Node node)
{
if (head == null) {
head = node;
}
else {
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = node;
}
}
void printList()
{
Node temp = head;
while (temp != null) {
Console.Write(temp.data + " ");
temp = temp.next;
}
Console.WriteLine();
}
public static void Main(String[] args)
{
MergeLists llist1 = new MergeLists();
MergeLists llist2 = new MergeLists();
llist1.addToTheLast(new Node(5));
llist1.addToTheLast(new Node(10));
llist1.addToTheLast(new Node(15));
llist2.addToTheLast(new Node(2));
llist2.addToTheLast(new Node(3));
llist2.addToTheLast(new Node(20));
llist1.head = new Gfg().sortedMerge(llist1.head,
llist2.head);
Console.WriteLine("Merged Linked List is:");
llist1.printList();
}
}
public class Gfg {
public Node sortedMerge(Node headA, Node headB)
{
Node dummyNode = new Node(0);
Node tail = dummyNode;
while (true) {
if (headA == null) {
tail.next = headB;
break;
}
if (headB == null) {
tail.next = headA;
break;
}
if (headA.data <= headB.data) {
tail.next = headA;
headA = headA.next;
}
else {
tail.next = headB;
headB = headB.next;
}
tail = tail.next;
}
return dummyNode.next;
}
}
|
Javascript
<script>
class Node
{
constructor(d)
{
this.data=d;
this.next = null;
}
}
class LinkedList
{
constructor()
{
this.head=null;
}
addToTheLast(node)
{
if (this.head == null)
{
this.head = node;
}
else
{
let temp = this.head;
while (temp.next != null)
temp = temp.next;
temp.next = node;
}
}
printList()
{
let temp = this.head;
while (temp != null)
{
document.write(temp.data + " ");
temp = temp.next;
}
document.write("<br>");
}
}
function sortedMerge(headA,headB)
{
let dummyNode = new Node(0);
let tail = dummyNode;
while(true)
{
if(headA == null)
{
tail.next = headB;
break;
}
if(headB == null)
{
tail.next = headA;
break;
}
if(headA.data <= headB.data)
{
tail.next = headA;
headA = headA.next;
}
else
{
tail.next = headB;
headB = headB.next;
}
tail = tail.next;
}
return dummyNode.next;
}
let llist1 = new LinkedList();
let llist2 = new LinkedList();
llist1.addToTheLast(new Node(5));
llist1.addToTheLast(new Node(10));
llist1.addToTheLast(new Node(15));
llist2.addToTheLast(new Node(2));
llist2.addToTheLast(new Node(3));
llist2.addToTheLast(new Node(20));
llist1.head = sortedMerge(llist1.head,
llist2.head);
document.write("Merged Linked List is:<br>")
llist1.printList();
</script>
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def printList(self):
temp = self.head
while temp:
print(temp.data, end=" ")
temp = temp.next
def addToList(self, newData):
newNode = Node(newData)
if self.head is None:
self.head = newNode
return
last = self.head
while last.next:
last = last.next
last.next = newNode
def mergeLists(headA, headB):
dummyNode = Node(0)
tail = dummyNode
while True:
if headA is None:
tail.next = headB
break
if headB is None:
tail.next = headA
break
if headA.data <= headB.data:
tail.next = headA
headA = headA.next
else:
tail.next = headB
headB = headB.next
tail = tail.next
return dummyNode.next
listA = LinkedList()
listB = LinkedList()
listA.addToList(5)
listA.addToList(10)
listA.addToList(15)
listB.addToList(2)
listB.addToList(3)
listB.addToList(20)
listA.head = mergeLists(listA.head, listB.head)
print("Merged Linked List is:")
listA.printList()
|
Output
Merged Linked List is:
2 3 5 10 15 20
Time Complexity: O(N + M), where N and M are the size of list1 and list2 respectively
Auxiliary Space: O(1)
Merge two sorted linked lists using Recursion:
The idea is to move ahead with node in the recursion whose node value is lesser. When any of the node reach the end then append the rest of the linked List.
Follow the steps below to solve the problem:
- Make a function where two pointers pointing to the linked list will be passed.
- Now, check which value is less from both the current nodes
- The one with less value makes a recursion call by moving ahead with that pointer and simultaneously append that recursion call with the node
- Also put two base cases to check whether one of the linked lists will reach the NULL, then append the rest of the linked list.
Below is the implementation of the above approach.
C
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node* next;
};
void MoveNode(struct Node** destRef,
struct Node** sourceRef);
struct Node* SortedMerge(struct Node* a, struct Node* b)
{
struct Node* result = NULL;
if (a == NULL)
return (b);
else if (b == NULL)
return (a);
if (a->data <= b->data) {
result = a;
result->next = SortedMerge(a->next, b);
}
else {
result = b;
result->next = SortedMerge(a, b->next);
}
return (result);
}
void MoveNode(struct Node** destRef,
struct Node** sourceRef)
{
struct Node* newNode = *sourceRef;
assert(newNode != NULL);
*sourceRef = newNode->next;
newNode->next = *destRef;
*destRef = newNode;
}
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node
= (struct Node*)malloc(sizeof(struct Node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void printList(struct Node* node)
{
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
int main()
{
struct Node* res = NULL;
struct Node* a = NULL;
struct Node* b = NULL;
push(&a, 15);
push(&a, 10);
push(&a, 5);
push(&b, 20);
push(&b, 3);
push(&b, 2);
res = SortedMerge(a, b);
printf("Merged Linked List is: \n");
printList(res);
return 0;
}
|
Java
import java.util.*;
class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
class MergeLists {
Node head;
public void addToTheLast(Node node)
{
if (head == null) {
head = node;
}
else {
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = node;
}
}
void printList()
{
System.out.println("Merged Linked List is:");
Node temp = head;
while (temp != null) {
System.out.print(temp.data + " ");
temp = temp.next;
}
System.out.println();
}
public static void main(String args[])
{
MergeLists llist1 = new MergeLists();
MergeLists llist2 = new MergeLists();
llist1.addToTheLast(new Node(5));
llist1.addToTheLast(new Node(10));
llist1.addToTheLast(new Node(15));
llist2.addToTheLast(new Node(2));
llist2.addToTheLast(new Node(3));
llist2.addToTheLast(new Node(20));
llist1.head = new Gfg().sortedMerge(llist1.head,
llist2.head);
llist1.printList();
}
}
class Gfg {
public Node sortedMerge(Node A, Node B)
{
if (A == null)
return B;
if (B == null)
return A;
if (A.data < B.data) {
A.next = sortedMerge(A.next, B);
return A;
}
else {
B.next = sortedMerge(A, B.next);
return B;
}
}
}
|
C#
using System;
public class Node {
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
}
}
public class MergeLists {
Node head;
public void addToTheLast(Node node)
{
if (head == null) {
head = node;
}
else {
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = node;
}
}
void printList()
{
Console.WriteLine("Merged Linked List is:");
Node temp = head;
while (temp != null) {
Console.Write(temp.data + " ");
temp = temp.next;
}
Console.WriteLine();
}
public static void Main(String[] args)
{
MergeLists llist1 = new MergeLists();
MergeLists llist2 = new MergeLists();
llist1.addToTheLast(new Node(5));
llist1.addToTheLast(new Node(10));
llist1.addToTheLast(new Node(15));
llist2.addToTheLast(new Node(2));
llist2.addToTheLast(new Node(3));
llist2.addToTheLast(new Node(20));
llist1.head = new Gfg().sortedMerge(llist1.head,
llist2.head);
llist1.printList();
}
}
public class Gfg {
public Node sortedMerge(Node A, Node B)
{
if (A == null)
return B;
if (B == null)
return A;
if (A.data < B.data) {
A.next = sortedMerge(A.next, B);
return A;
}
else {
B.next = sortedMerge(A, B.next);
return B;
}
}
}
|
Javascript
<script>
function SortedMerge( A, B) {
if (A == null)
return B;
if (B == null)
return A;
if (A.data < B.data) {
A.next = SortedMerge(A.next, B);
return A;
} else {
B.next = SortedMerge(A, B.next);
return B;
}
}
</script>
|
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
};
Node* SortedMerge(Node* a, Node* b)
{
Node* result = NULL;
if (a == NULL)
return (b);
else if (b == NULL)
return (a);
if (a->data <= b->data) {
result = a;
result->next = SortedMerge(a->next, b);
}
else {
result = b;
result->next = SortedMerge(a, b->next);
}
return (result);
}
void push(Node** head_ref, int new_data)
{
Node* new_node = new Node();
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
void printList(Node* node)
{
while (node != NULL) {
cout << node->data << " ";
node = node->next;
}
}
int main()
{
Node* res = NULL;
Node* a = NULL;
Node* b = NULL;
push(&a, 15);
push(&a, 10);
push(&a, 5);
push(&b, 20);
push(&b, 3);
push(&b, 2);
res = SortedMerge(a, b);
cout << "Merged Linked List is: \n";
printList(res);
return 0;
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def printList(self):
temp = self.head
while temp:
print(temp.data, end=" ")
temp = temp.next
def append(self, new_data):
new_node = Node(new_data)
if self.head is None:
self.head = new_node
return
last = self.head
while last.next:
last = last.next
last.next = new_node
def mergeLists(head1, head2):
temp = None
if head1 is None:
return head2
if head2 is None:
return head1
if head1.data <= head2.data:
temp = head1
temp.next = mergeLists(head1.next, head2)
else:
temp = head2
temp.next = mergeLists(head1, head2.next)
return temp
if __name__ == '__main__':
list1 = LinkedList()
list1.append(5)
list1.append(10)
list1.append(15)
list2 = LinkedList()
list2.append(2)
list2.append(3)
list2.append(20)
list3 = LinkedList()
list3.head = mergeLists(list1.head, list2.head)
print("Merged Linked List is:")
list3.printList()
|
Output
Merged Linked List is:
2 3 5 10 15 20
Time Complexity: O(M + N), Where M and N are the size of the list1 and list2 respectively.
Auxiliary Space: O(M+N), Function call stack space
Merge two sorted linked lists by Reversing the Lists:
This idea involves first reversing both the given lists and after reversing, traversing both the lists till the end and then comparing the nodes of both the lists and inserting the node with a larger value at the beginning of the result list. And in this way, we will get the resulting list in increasing order.
Follow the steps below to solve the problem:
- Initialize result list as empty: head = NULL.
- Let ‘a’ and ‘b’ be the heads of the first and second lists respectively.
- Reverse both lists.
- While (a != NULL and b != NULL)
- Find the larger of two (Current ‘a’ and ‘b’)
- Insert the larger value of the node at the front of result list.
- Move ahead in the list with the larger node.
- If ‘b’ becomes NULL before ‘a’, insert all nodes of ‘a’ into result list at the beginning.
- If ‘a’ becomes NULL before ‘b’, insert all nodes of ‘b’ into result list at the beginning.
Below is the implementation of the above solution.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node* next;
};
Node* reverseList(Node* head)
{
if (head->next == NULL)
return head;
Node* rest = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return rest;
}
Node* sortedMerge(Node* a, Node* b)
{
a = reverseList(a);
b = reverseList(b);
Node* head = NULL;
Node* temp;
while (a != NULL && b != NULL) {
if (a->key >= b->key) {
temp = a->next;
a->next = head;
head = a;
a = temp;
}
else {
temp = b->next;
b->next = head;
head = b;
b = temp;
}
}
while (a != NULL) {
temp = a->next;
a->next = head;
head = a;
a = temp;
}
while (b != NULL) {
temp = b->next;
b->next = head;
head = b;
b = temp;
}
return head;
}
void printList(struct Node* Node)
{
while (Node != NULL) {
cout << Node->key << " ";
Node = Node->next;
}
}
Node* newNode(int key)
{
Node* temp = new Node;
temp->key = key;
temp->next = NULL;
return temp;
}
int main()
{
struct Node* res = NULL;
Node* a = newNode(5);
a->next = newNode(10);
a->next->next = newNode(15);
a->next->next->next = newNode(40);
Node* b = newNode(2);
b->next = newNode(3);
b->next->next = newNode(20);
res = sortedMerge(a, b);
cout << "Merged Linked List is:" << endl;
printList(res);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
typedef struct Node {
int key;
struct Node* next;
} Node;
Node* reverseList(Node* head)
{
if (head->next == NULL)
return head;
Node* rest = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return rest;
}
Node* sortedMerge(Node* a, Node* b)
{
a = reverseList(a);
b = reverseList(b);
Node* head = NULL;
Node* temp;
while (a != NULL && b != NULL) {
if (a->key >= b->key) {
temp = a->next;
a->next = head;
head = a;
a = temp;
}
else {
temp = b->next;
b->next = head;
head = b;
b = temp;
}
}
while (a != NULL) {
temp = a->next;
a->next = head;
head = a;
a = temp;
}
while (b != NULL) {
temp = b->next;
b->next = head;
head = b;
b = temp;
}
return head;
}
void printList(struct Node* Node)
{
while (Node != NULL) {
printf("%d ", Node->key);
Node = Node->next;
}
}
Node* newNode(int key)
{
Node* temp = (Node*)malloc(sizeof(Node));
temp->key = key;
temp->next = NULL;
return temp;
}
int main()
{
struct Node* res = NULL;
Node* a = newNode(5);
a->next = newNode(10);
a->next->next = newNode(15);
a->next->next->next = newNode(40);
Node* b = newNode(2);
b->next = newNode(3);
b->next->next = newNode(20);
res = sortedMerge(a, b);
printf("Merged Linked List is: \n");
printList(res);
return 0;
}
|
Java
import java.util.*;
class GFG {
static class Node {
int key;
Node next;
};
static Node reverseList(Node head)
{
if (head.next == null)
return head;
Node rest = reverseList(head.next);
head.next.next = head;
head.next = null;
return rest;
}
static Node sortedMerge(Node a, Node b)
{
a = reverseList(a);
b = reverseList(b);
Node head = null;
Node temp;
while (a != null && b != null) {
if (a.key >= b.key) {
temp = a.next;
a.next = head;
head = a;
a = temp;
}
else {
temp = b.next;
b.next = head;
head = b;
b = temp;
}
}
while (a != null) {
temp = a.next;
a.next = head;
head = a;
a = temp;
}
while (b != null) {
temp = b.next;
b.next = head;
head = b;
b = temp;
}
return head;
}
static void printList(Node Node)
{
while (Node != null) {
System.out.print(Node.key + " ");
Node = Node.next;
}
}
static Node newNode(int key)
{
Node temp = new Node();
temp.key = key;
temp.next = null;
return temp;
}
public static void main(String[] args)
{
Node res = null;
Node a = newNode(5);
a.next = newNode(10);
a.next.next = newNode(15);
a.next.next.next = newNode(40);
Node b = newNode(2);
b.next = newNode(3);
b.next.next = newNode(20);
res = sortedMerge(a, b);
System.out.println("Merged Linked List is:");
printList(res);
}
}
|
C#
using System;
using System.Collections.Generic;
public class GFG {
public class Node {
public int key;
public Node next;
};
static Node reverseList(Node head)
{
if (head.next == null)
return head;
Node rest = reverseList(head.next);
head.next.next = head;
head.next = null;
return rest;
}
static Node sortedMerge(Node a, Node b)
{
a = reverseList(a);
b = reverseList(b);
Node head = null;
Node temp;
while (a != null && b != null) {
if (a.key >= b.key) {
temp = a.next;
a.next = head;
head = a;
a = temp;
}
else {
temp = b.next;
b.next = head;
head = b;
b = temp;
}
}
while (a != null) {
temp = a.next;
a.next = head;
head = a;
a = temp;
}
while (b != null) {
temp = b.next;
b.next = head;
head = b;
b = temp;
}
return head;
}
static void printList(Node Node)
{
while (Node != null) {
Console.Write(Node.key + " ");
Node = Node.next;
}
}
static Node newNode(int key)
{
Node temp = new Node();
temp.key = key;
temp.next = null;
return temp;
}
public static void Main(String[] args)
{
Node res = null;
Node a = newNode(5);
a.next = newNode(10);
a.next.next = newNode(15);
a.next.next.next = newNode(40);
Node b = newNode(2);
b.next = newNode(3);
b.next.next = newNode(20);
res = sortedMerge(a, b);
Console.WriteLine("Merged Linked List is:");
printList(res);
}
}
|
Javascript
class Node {
constructor(key) {
this.key = key;
this.next = null;
}
}
function reverseList(head) {
if (!head.next) {
return head;
}
const rest = reverseList(head.next);
head.next.next = head;
head.next = null;
return rest;
}
function sortedMerge(a, b) {
a = reverseList(a);
b = reverseList(b);
let head = null;
let temp;
while (a && b) {
if (a.key >= b.key) {
temp = a.next;
a.next = head;
head = a;
a = temp;
}
else {
temp = b.next;
b.next = head;
head = b;
b = temp;
}
}
while (a) {
temp = a.next;
a.next = head;
head = a;
a = temp;
}
while (b) {
temp = b.next;
b.next = head;
head = b;
b = temp;
}
return head;
}
function printList(node) {
let result = "";
while (node) {
result += node.key + " ";
node = node.next;
}
console.log(result);
}
let res = null;
const a = new Node(5);
a.next = new Node(10);
a.next.next = new Node(15);
a.next.next.next = new Node(40);
const b = new Node(2);
b.next = new Node(3);
b.next.next = new Node(20);
res = sortedMerge(a, b);
console.log("Merged Linked List is:" + "<br>");
printList(res);
|
Python3
class Node:
def __init__(self, key):
self.key = key
self.next = None
def reverse_list(head):
if head.next is None:
return head
rest = reverse_list(head.next)
head.next.next = head
head.next = None
return rest
def sorted_merge(a, b):
a = reverse_list(a)
b = reverse_list(b)
head = None
while a is not None and b is not None:
if a.key >= b.key:
temp = a.next
a.next = head
head = a
a = temp
else:
temp = b.next
b.next = head
head = b
b = temp
while a is not None:
temp = a.next
a.next = head
head = a
a = temp
while b is not None:
temp = b.next
b.next = head
head = b
b = temp
return head
def print_list(node):
while node is not None:
print(node.key, end=" ")
node = node.next
print()
def new_node(key):
temp = Node(key)
return temp
res = None
a = new_node(5)
a.next = new_node(10)
a.next.next = new_node(15)
a.next.next.next = new_node(40)
b = new_node(2)
b.next = new_node(3)
b.next.next = new_node(20)
res = sorted_merge(a, b)
print("Merged Linked List is:")
print_list(res)
|
Output
Merged Linked List is:
2 3 5 10 15 20 40
Time Complexity: O(M+N) where M and N are the lengths of the two lists to be merged.
Auxiliary Space: O(M+N)
This method is contributed by Mehul Mathur(mathurmehul01).
Please refer below post for simpler implementations :
Merge two sorted lists (in-place)
Please write comments if you find the above code/algorithm incorrect, or find better ways to solve the same problem.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...