Merge Sort for Linked Lists
Last Updated :
22 Apr, 2024
Merge sort is often preferred for sorting a linked list. The slow random-access performance of a linked list makes other algorithms like Quick Sort perform poorly, and other like Heap Sort completely impossible.
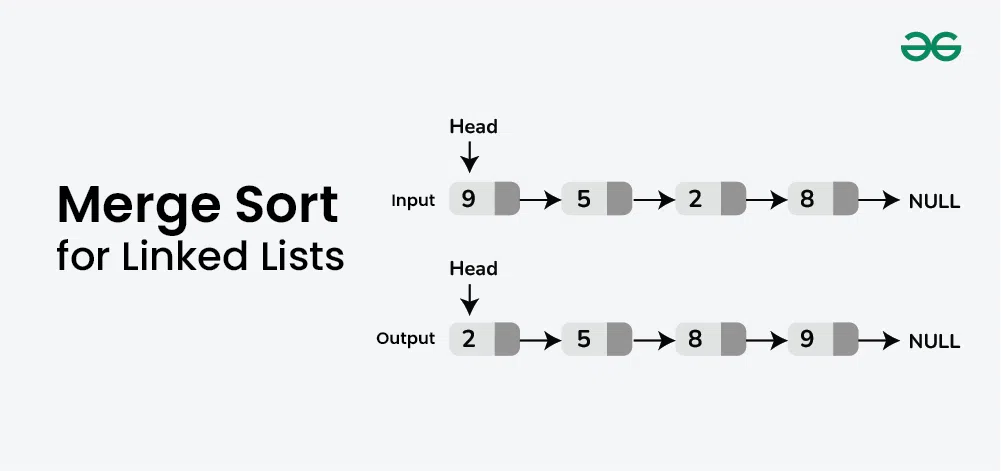
Examples:
Input: 40 -> 20 -> 60 -> 10 -> 50 -> 30 -> NULL
Output: 10 -> 20 -> 30 -> 40 -> 50 -> 60 -> NULL
Input: 9 -> 5 -> 2 -> 8 -> NULL
Output: 2 -> 5 -> 8 -> 9 -> NULL
Approach: To solve the problem, follow the below idea:
Maintain a function say MergeSort(headRef) that takes reference to the head of a linked list and sorts the linked list using Merge Sort.
Inside the MergeSort(headRef), we sort the linked list in three phases:
- Divide the linked list into two halves: Divide the linked list into two halves, say first and second. This can be done by finding the middle node of the linked list, say mid. Now, the first list will be from head to the node just before mid and the second list will be from mid till the end of the list.
- Recursively Sort the two halves: Call the MergeSort(first) and MergeSort(second) to recursively sort the individual linked lists.
- Merge the two sorted halves: Now, merge the two sorted linked list into a single sorted linked list and return it.
Note that we need a reference to head in MergeSort() as the head node has to be changed if the data at the original head is not the smallest value in the linked list.
Step-by-step algorithm:
- Let head be the first node of the linked list to be sorted and headRef be the pointer to head.
- Define a function, say MergeSort(headRef)
- If the head is NULL or there is only one element in the linked list then return.
- Else divide the linked list into two halves, say first and second.
- Sort the two halves first and second.
- Call MergeSort(first) and MergeSort(second) to recursively sort the two halves.
- Merge the sorted halves first and second using SortedMerge() and update the head pointer using headRef.
Below is the implementation of the algorithm:
C
// C code for linked list merged sort
#include <stdio.h>
#include <stdlib.h>
/* Link list node */
struct Node {
int data;
struct Node* next;
};
/* function prototypes */
struct Node* SortedMerge(struct Node* a, struct Node* b);
void FrontBackSplit(struct Node* source,
struct Node** frontRef, struct Node** backRef);
/* sorts the linked list by changing next pointers (not data) */
void MergeSort(struct Node** headRef)
{
struct Node* head = *headRef;
struct Node* a;
struct Node* b;
/* Base case -- length 0 or 1 */
if ((head == NULL) || (head->next == NULL)) {
return;
}
/* Split head into 'a' and 'b' sublists */
FrontBackSplit(head, &a, &b);
/* Recursively sort the sublists */
MergeSort(&a);
MergeSort(&b);
/* answer = merge the two sorted lists together */
*headRef = SortedMerge(a, b);
}
/* See https://www.geeksforgeeks.org/merge-two-sorted-linked-lists/
for details of this function */
struct Node* SortedMerge(struct Node* a, struct Node* b)
{
struct Node* result = NULL;
/* Base cases */
if (a == NULL)
return (b);
else if (b == NULL)
return (a);
/* Pick either a or b, and recur */
if (a->data <= b->data) {
result = a;
result->next = SortedMerge(a->next, b);
}
else {
result = b;
result->next = SortedMerge(a, b->next);
}
return (result);
}
/* UTILITY FUNCTIONS */
/* Split the nodes of the given list into front and back halves,
and return the two lists using the reference parameters.
If the length is odd, the extra node should go in the front list.
Uses the fast/slow pointer strategy. */
void FrontBackSplit(struct Node* source,
struct Node** frontRef, struct Node** backRef)
{
struct Node* fast;
struct Node* slow;
slow = source;
fast = source->next;
/* Advance 'fast' two nodes, and advance 'slow' one node */
while (fast != NULL) {
fast = fast->next;
if (fast != NULL) {
slow = slow->next;
fast = fast->next;
}
}
/* 'slow' is before the midpoint in the list, so split it in two
at that point. */
*frontRef = source;
*backRef = slow->next;
slow->next = NULL;
}
/* Function to print nodes in a given linked list */
void printList(struct Node* node)
{
while (node != NULL) {
printf("%d ", node->data);
node = node->next;
}
}
/* Function to insert a node at the beginning of the linked list */
void push(struct Node** head_ref, int new_data)
{
/* allocate node */
struct Node* new_node = (struct Node*)malloc(sizeof(struct Node));
/* put in the data */
new_node->data = new_data;
/* link the old list of the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
/* Driver program to test above functions*/
int main()
{
/* Start with the empty list */
struct Node* res = NULL;
struct Node* a = NULL;
/* Let us create a unsorted linked lists to test the functions
Created lists shall be a: 2->3->20->5->10->15 */
push(&a, 15);
push(&a, 10);
push(&a, 5);
push(&a, 20);
push(&a, 3);
push(&a, 2);
/* Sort the above created Linked List */
MergeSort(&a);
printf("Sorted Linked List is: \n");
printList(a);
getchar();
return 0;
}
// Java program to illustrate merge sorted
// of linkedList
public class linkedList {
node head = null;
// node a, b;
static class node {
int val;
node next;
public node(int val)
{
this.val = val;
}
}
node sortedMerge(node a, node b)
{
node result = null;
/* Base cases */
if (a == null)
return b;
if (b == null)
return a;
/* Pick either a or b, and recur */
if (a.val <= b.val) {
result = a;
result.next = sortedMerge(a.next, b);
}
else {
result = b;
result.next = sortedMerge(a, b.next);
}
return result;
}
node mergeSort(node h)
{
// Base case : if head is null
if (h == null || h.next == null) {
return h;
}
// get the middle of the list
node middle = getMiddle(h);
node nextofmiddle = middle.next;
// set the next of middle node to null
middle.next = null;
// Apply mergeSort on left list
node left = mergeSort(h);
// Apply mergeSort on right list
node right = mergeSort(nextofmiddle);
// Merge the left and right lists
node sortedlist = sortedMerge(left, right);
return sortedlist;
}
// Utility function to get the middle of the linked list
public static node getMiddle(node head)
{
if (head == null)
return head;
node slow = head, fast = head;
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
void push(int new_data)
{
/* allocate node */
node new_node = new node(new_data);
/* link the old list of the new node */
new_node.next = head;
/* move the head to point to the new node */
head = new_node;
}
// Utility function to print the linked list
void printList(node headref)
{
while (headref != null) {
System.out.print(headref.val + " ");
headref = headref.next;
}
}
public static void main(String[] args)
{
linkedList li = new linkedList();
/*
* Let us create a unsorted linked list to test the functions
* created. The list shall be a: 2->3->20->5->10->15
*/
li.push(15);
li.push(10);
li.push(5);
li.push(20);
li.push(3);
li.push(2);
// Apply merge Sort
li.head = li.mergeSort(li.head);
System.out.print("\n Sorted Linked List is: \n");
li.printList(li.head);
}
}
// This code is contributed by Rishabh Mahrsee
# Python3 program to merge sort of linked list
# create Node using class Node.
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
# push new value to linked list
# using append method
def append(self, new_value):
# Allocate new node
new_node = Node(new_value)
# if head is None, initialize it to new node
if self.head is None:
self.head = new_node
return
curr_node = self.head
while curr_node.next is not None:
curr_node = curr_node.next
# Append the new node at the end
# of the linked list
curr_node.next = new_node
def sortedMerge(self, a, b):
result = None
# Base cases
if a == None:
return b
if b == None:
return a
# pick either a or b and recur..
if a.data <= b.data:
result = a
result.next = self.sortedMerge(a.next, b)
else:
result = b
result.next = self.sortedMerge(a, b.next)
return result
def mergeSort(self, h):
# Base case if head is None
if h == None or h.next == None:
return h
# get the middle of the list
middle = self.getMiddle(h)
nexttomiddle = middle.next
# set the next of middle node to None
middle.next = None
# Apply mergeSort on left list
left = self.mergeSort(h)
# Apply mergeSort on right list
right = self.mergeSort(nexttomiddle)
# Merge the left and right lists
sortedlist = self.sortedMerge(left, right)
return sortedlist
# Utility function to get the middle
# of the linked list
def getMiddle(self, head):
if (head == None):
return head
slow = head
fast = head
while (fast.next != None and
fast.next.next != None):
slow = slow.next
fast = fast.next.next
return slow
# Utility function to print the linked list
def printList(head):
if head is None:
print(' ')
return
curr_node = head
while curr_node:
print(curr_node.data, end = " ")
curr_node = curr_node.next
print(' ')
# Driver Code
if __name__ == '__main__':
li = LinkedList()
# Let us create a unsorted linked list
# to test the functions created.
# The list shall be a: 2->3->20->5->10->15
li.append(15)
li.append(10)
li.append(5)
li.append(20)
li.append(3)
li.append(2)
# Apply merge Sort
li.head = li.mergeSort(li.head)
print ("Sorted Linked List is:")
printList(li.head)
# This code is contributed by Vikas Chitturi
// C# program to illustrate merge sorted
// of linkedList
using System;
public class linkedList {
node head = null;
// node a, b;
public class node {
public int val;
public node next;
public node(int val)
{
this.val = val;
}
}
node sortedMerge(node a, node b)
{
node result = null;
/* Base cases */
if (a == null)
return b;
if (b == null)
return a;
/* Pick either a or b, and recur */
if (a.val <= b.val) {
result = a;
result.next = sortedMerge(a.next, b);
}
else {
result = b;
result.next = sortedMerge(a, b.next);
}
return result;
}
node mergeSort(node h)
{
// Base case : if head is null
if (h == null || h.next == null) {
return h;
}
// get the middle of the list
node middle = getMiddle(h);
node nextofmiddle = middle.next;
// set the next of middle node to null
middle.next = null;
// Apply mergeSort on left list
node left = mergeSort(h);
// Apply mergeSort on right list
node right = mergeSort(nextofmiddle);
// Merge the left and right lists
node sortedlist = sortedMerge(left, right);
return sortedlist;
}
// Utility function to get the
// middle of the linked list
node getMiddle(node h)
{
// Base case
if (h == null)
return h;
node fastptr = h.next;
node slowptr = h;
// Move fastptr by two and slow ptr by one
// Finally slowptr will point to middle node
while (fastptr != null) {
fastptr = fastptr.next;
if (fastptr != null) {
slowptr = slowptr.next;
fastptr = fastptr.next;
}
}
return slowptr;
}
void push(int new_data)
{
/* allocate node */
node new_node = new node(new_data);
/* link the old list of the new node */
new_node.next = head;
/* move the head to point to the new node */
head = new_node;
}
// Utility function to print the linked list
void printList(node headref)
{
while (headref != null) {
Console.Write(headref.val + " ");
headref = headref.next;
}
}
// Driver code
public static void Main(String[] args)
{
linkedList li = new linkedList();
/*
* Let us create a unsorted linked list to test the functions
* created. The list shall be a: 2->3->20->5->10->15
*/
li.push(15);
li.push(10);
li.push(5);
li.push(20);
li.push(3);
li.push(2);
// Apply merge Sort
li.head = li.mergeSort(li.head);
Console.Write("\n Sorted Linked List is: \n");
li.printList(li.head);
}
}
// This code is contributed by Arnab Kundu
// Javascript program to
// illustrate merge sorted
// of linkedList
var head = null;
// node a, b;
class node {
constructor(val) {
this.val = val;
this.next = null;
}
}
function sortedMerge( a, b)
{
var result = null;
/* Base cases */
if (a == null)
return b;
if (b == null)
return a;
/* Pick either a or b, and recur */
if (a.val <= b.val) {
result = a;
result.next = sortedMerge(a.next, b);
} else {
result = b;
result.next = sortedMerge(a, b.next);
}
return result;
}
function mergeSort( h) {
// Base case : if head is null
if (h == null || h.next == null) {
return h;
}
// get the middle of the list
var middle = getMiddle(h);
var nextofmiddle = middle.next;
// set the next of middle node to null
middle.next = null;
// Apply mergeSort on left list
var left = mergeSort(h);
// Apply mergeSort on right list
var right = mergeSort(nextofmiddle);
// Merge the left and right lists
var sortedlist = sortedMerge(left, right);
return sortedlist;
}
// Utility function to get the middle
// of the linked list
function getMiddle( head) {
if (head == null)
return head;
var slow = head, fast = head;
while (fast.next != null && fast.next.next != null)
{
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
function push(new_data) {
/* allocate node */
var new_node = new node(new_data);
/* link the old list of the new node */
new_node.next = head;
/* move the head to point to the new node */
head = new_node;
}
// Utility function to print the linked list
function printList( headref) {
while (headref != null) {
document.write(headref.val + " ");
headref = headref.next;
}
}
/*
Let us create a unsorted linked
list to test the functions
created. The list shall be
a: 2->3->20->5->10->15
*/
push(15);
push(10);
push(5);
push(20);
push(3);
push(2);
// Apply merge Sort
head = mergeSort(head);
console.log("\n Sorted Linked List is: \n");
printList(head);
// This code contributed by umadevi9616
#include <bits/stdc++.h>
using namespace std;
/* Link list node */
class Node {
public:
int data;
Node* next;
Node(int x) { data = x; }
};
/* See https:// www.geeksforgeeks.org/?p=3622 for details of
this function */
Node* SortedMerge(Node* first, Node* second)
{
Node* result = NULL;
/* Base cases */
if (first == NULL)
return (second);
else if (second == NULL)
return (first);
/* Pick either a or b, and recur */
if (first->data <= second->data) {
result = first;
result->next = SortedMerge(first->next, second);
}
else {
result = second;
result->next = SortedMerge(first, second->next);
}
return (result);
}
/* UTILITY FUNCTIONS */
/* Split the nodes of the given list into first and second
halves, and return the two lists using the reference
parameters. If the length is odd, the extra node should
go in the first list. Uses the fast/slow pointer
strategy. */
void splitList(Node* source, Node** firstRef,
Node** secondRef)
{
Node* slow = source;
Node* fast = source->next;
/* Advance 'fast' two nodes, and advance 'slow' one node
*/
while (fast != NULL) {
fast = fast->next;
if (fast != NULL) {
slow = slow->next;
fast = fast->next;
}
}
/* 'slow' is before the midpoint in the list, so split
it in two at that point. */
*firstRef = source;
*secondRef = slow->next;
slow->next = NULL;
}
/* sorts the linked list by changing next pointers (not
* data) */
void MergeSort(Node** headRef)
{
Node* head = *headRef;
Node* first;
Node* second;
/* Base case -- length 0 or 1 */
if ((head == NULL) || (head->next == NULL)) {
return;
}
/* Split head into 'first' and 'second' sublists */
splitList(head, &first, &second);
/* Recursively sort the sublists */
MergeSort(&first);
MergeSort(&second);
/* answer = merge the two sorted lists together */
*headRef = SortedMerge(first, second);
}
/* Function to print nodes in a given linked list */
void printList(Node* node)
{
while (node != NULL) {
cout << node->data << " ";
node = node->next;
}
}
/* Function to insert a node at the beginning of the linked
* list */
void push(Node** head_ref, int new_data)
{
/* allocate node */
Node* new_node = new Node(new_data);
/* link the old list of the new node */
new_node->next = (*head_ref);
/* move the head to point to the new node */
(*head_ref) = new_node;
}
/* Driver program to test above functions*/
int main()
{
/* Start with the empty list */
Node* head = NULL;
/* Let us create a unsorted linked lists to test the
functions Created lists shall be a:
2->3->20->5->10->15 */
push(&head, 15);
push(&head, 10);
push(&head, 5);
push(&head, 20);
push(&head, 3);
push(&head, 2);
/* Sort the above created Linked List */
MergeSort(&head);
cout << "Sorted Linked List is: \n";
printList(head);
return 0;
}
// This is code is contributed by rathbhupendra
OutputSorted Linked List is:
2 3 5 10 15 20
Time Complexity: O(N*logN)
Auxiliary Space: O(logN)
Approach: To solve the problem, follow the below idea:
In this, we will use bottom-up approach because we start with sublists of size 1, then merge adjacent sublists, doubling the size of sublists in each iteration until the entire list is sorted.
We will start by having lists of one element and from thereon keep merging those, doubling their sizes at each stage up to when all the elements are properly ordered.
Step-by-step algorithm:
- Begin with a sublist size of 1.
- Iterate over the list and merge adjacent sublists that are currently that size.
- Double the sizes of sublists upon every iteration until the whole list gets sorted out.
Below is the implementation of the algorithm:
Java
class ListNode {
int value;
ListNode next;
ListNode(int value) {
this.value = value;
this.next = null;
}
}
public class Main {
public static void main(String[] args) {
// Example 1
ListNode head1 = new ListNode(15);
head1.next = new ListNode(10);
head1.next.next = new ListNode(5);
head1.next.next.next = new ListNode(20);
head1.next.next.next.next = new ListNode(3);
head1.next.next.next.next.next = new ListNode(2);
ListNode sortedHead1 = mergeSortBottomUp(head1);
System.out.println("Sorted List:");
printList(sortedHead1);
}
public static ListNode mergeSortBottomUp(ListNode head) {
if (head == null || head.next == null) {
return head;
}
int length = getLength(head);
int size = 1;
ListNode dummy = new ListNode(0);
dummy.next = head;
while (size < length) {
ListNode current = dummy.next;
ListNode tail = dummy;
while (current != null) {
ListNode left = current;
ListNode right = split(left, size);
current = split(right, size);
tail = merge(left, right, tail);
}
size *= 2;
}
return dummy.next;
}
public static int getLength(ListNode head) {
int length = 0;
while (head != null) {
length++;
head = head.next;
}
return length;
}
public static ListNode split(ListNode head, int size) {
if (head == null) {
return null;
}
for (int i = 0; i < size - 1 && head.next != null; i++) {
head = head.next;
}
ListNode nextHead = head.next;
head.next = null;
return nextHead;
}
public static ListNode merge(ListNode left, ListNode right, ListNode head) {
ListNode current = head;
while (left != null && right != null) {
if (left.value < right.value) {
current.next = left;
left = left.next;
} else {
current.next = right;
right = right.next;
}
current = current.next;
}
current.next = (left != null) ? left : right;
while (current.next != null) {
current = current.next;
}
return current;
}
// Utility function to print the linked list
public static void printList(ListNode head) {
while (head != null) {
System.out.print(head.value + " -> ");
head = head.next;
}
System.out.println("NULL");
}
}
class ListNode:
def __init__(self, value=0, next=None):
self.value = value
self.next = next
def merge_sort_bottom_up(head):
if not head or not head.next:
return head
length = get_length(head)
size = 1
dummy = ListNode()
dummy.next = head
while size < length:
current = dummy.next
tail = dummy
while current:
left = current
right = split(left, size)
current = split(right, size)
tail = merge(left, right, tail)
size *= 2
return dummy.next
def get_length(head):
length = 0
while head:
length += 1
head = head.next
return length
def split(head, size):
if not head:
return None
for _ in range(size - 1):
if head.next:
head = head.next
else:
break
next_head = head.next
head.next = None
return next_head
def merge(left, right, head):
current = head
while left and right:
if left.value < right.value:
current.next = left
left = left.next
else:
current.next = right
right = right.next
current = current.next
current.next = left if left else right
while current.next:
current = current.next
return current
# Utility function to print the linked list
def print_list(head):
while head:
print(head.value, end=" -> ")
head = head.next
print("NULL")
# Example usage
if __name__ == "__main__":
# Example 1
head1 = ListNode(15)
head1.next = ListNode(10)
head1.next.next = ListNode(5)
head1.next.next.next = ListNode(20)
head1.next.next.next.next = ListNode(3)
head1.next.next.next.next.next = ListNode(2)
sorted_head1 = merge_sort_bottom_up(head1)
print("Sorted List:")
print_list(sorted_head1)
class ListNode {
constructor(value = 0, next = null) {
this.value = value;
this.next = next;
}
}
function mergeSortBottomUp(head) {
if (!head || !head.next) {
return head;
}
let length = getLength(head);
let size = 1;
let dummy = new ListNode();
dummy.next = head;
while (size < length) {
let current = dummy.next;
let tail = dummy;
while (current) {
let left = current;
let right = split(left, size);
current = split(right, size);
tail = merge(left, right, tail);
}
size *= 2;
}
return dummy.next;
}
function getLength(head) {
let length = 0;
while (head) {
length++;
head = head.next;
}
return length;
}
function split(head, size) {
if (!head) {
return null;
}
for (let i = 1; i < size && head.next; i++) {
head = head.next;
}
let nextHead = head.next;
head.next = null;
return nextHead;
}
function merge(left, right, head) {
let current = head;
while (left && right) {
if (left.value < right.value) {
current.next = left;
left = left.next;
} else {
current.next = right;
right = right.next;
}
current = current.next;
}
current.next = left || right;
while (current.next) {
current = current.next;
}
return current;
}
// Utility function to print the linked list
function printList(head) {
let result = "";
while (head) {
result += head.value + " -> ";
head = head.next;
}
result += "NULL";
console.log(result);
}
// Example usage
// Example 1
let head1 = new ListNode(15);
head1.next = new ListNode(10);
head1.next.next = new ListNode(5);
head1.next.next.next = new ListNode(20);
head1.next.next.next.next = new ListNode(3);
head1.next.next.next.next.next = new ListNode(2);
let sortedHead1 = mergeSortBottomUp(head1);
console.log("Sorted List:");
printList(sortedHead1);
OutputSorted List:
2 -> 3 -> 5 -> 10 -> 15 -> 20 -> NULL
Time Complexity: O(N*logN)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...