Lagrange’s Mean Value Theorem

Suppose 

be a function satisfying these conditions:

1) f(x) is continuous in the closed interval a ≤ x ≤ b

2) f(x) is differentiable in the open interval a < x < b

Then according to Lagrange’s Theorem, there exists at least one point ‘c’ in the open interval (a, b) such that:

 We can visualize Lagrange’s Theorem by the following figure

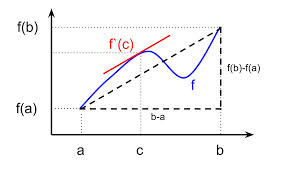
In simple words, Lagrange’s theorem says that if there is a path between two points A(a, f(a)) and B(b, f(a)) in a 2-D plain then there will be at least one point ‘c’ on the path such that the slope of the tangent at point ‘c’, i.e., (f ‘ (c)) is equal to the average slope of the path, i.e., 

Example: Verify mean value theorem for f(x) = x² in interval [2,4]. 

Solution: First check if the function is continuous in the given closed interval, the answer is Yes. Then check for differentiability in the open interval (2,4), Yes it is differentiable. 

f(2) = 4 

and f(4) = 16 

Mean value theorem states that there is a point c ∈ (2, 4) such that 

But 

which implies c = 3. Thus at c = 3 ∈ (2, 4), we have 

This article has been contributed by Saurabh Sharma. 

If you would like to contribute, please email us your interest at review-team@geeksforgeeks.org 

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above