k-th smallest absolute difference of two elements in an array
Last Updated :
21 Aug, 2022
We are given an array of size n containing positive integers. The absolute difference between values at indices i and j is |a[i] – a[j]|. There are n*(n-1)/2 such pairs and we are asked to print the kth (1 <= k <= n*(n-1)/2) as the smallest absolute difference among all these pairs.
Examples:
Input : a[] = {1, 2, 3, 4}
k = 3
Output : 1
The possible absolute differences are :
{1, 2, 3, 1, 2, 1}.
The 3rd smallest value among these is 1.Input : n = 2
a[] = {10, 10}
k = 1
Output : 0
Naive Method is to find all the n*(n-1)/2 possible absolute differences in O(n^2) and store them in an array. Then sort this array and print the kth minimum value from this array. This will take time O(n^2 + n^2 * log(n^2)) = O(n^2 + 2*n^2*log(n)).
The naive method won’t be efficient for large values of n, say n = 10^5.
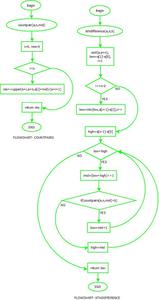
An Efficient Solution is based on Binary Search.
1) Sort the given array a[].
2) We can easily find the least possible absolute
difference in O(n) after sorting. The largest
possible difference will be a[n-1] - a[0] after
sorting the array. Let low = minimum_difference
and high = maximum_difference.
3) while low < high:
4) mid = (low + high)/2
5) if ((number of pairs with absolute difference
<= mid) < k):
6) low = mid + 1
7) else:
8) high = mid
9) return low
We need a function that will tell us the number of pairs with a difference <= mid efficiently. Since our array is sorted, this part can be done like this:
1) result = 0
2) for i = 0 to n-1:
3) result = result + (upper_bound(a+i, a+n, a[i] + mid) - (a+i+1))
4) return result
Here upper_bound is a variant of binary search that returns a pointer to the first element from a[i] to a[n-1] which is greater than a[i] + mid. Let the pointer returned be j. Then a[i] + mid < a[j]. Thus, subtracting (a+i+1) from this will give us the number of values whose difference with a[i] is <= mid. We sum this up for all indices from 0 to n-1 and get the answer for the current mid.
Flowchart is as follows:
Flowchart
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
int countPairs(int *a, int n, int mid)
{
int res = 0;
for (int i = 0; i < n; ++i)
res += upper_bound(a+i, a+n, a[i] + mid) -
(a + i + 1);
return res;
}
int kthDiff(int a[], int n, int k)
{
sort(a, a+n);
int low = a[1] - a[0];
for (int i = 1; i <= n-2; ++i)
low = min(low, a[i+1] - a[i]);
int high = a[n-1] - a[0];
while (low < high)
{
int mid = (low+high)>>1;
if (countPairs(a, n, mid) < k)
low = mid + 1;
else
high = mid;
}
return low;
}
int main()
{
int k = 3;
int a[] = {1, 2, 3, 4};
int n = sizeof(a)/sizeof(a[0]);
cout << kthDiff(a, n, k);
return 0;
}
|
Java
import java.util.Scanner;
import java.util.Arrays;
class GFG
{
static int countPairs(int[] a, int n, int mid)
{
int res = 0, value;
for(int i = 0; i < n; i++)
{
if(a[i]+mid>a[n-1])
res+=(n-(i+1));
else
{
int ub = upperbound(a, n, a[i]+mid);
res += (ub- (i+1));
}
}
return res;
}
static int upperbound(int a[], int n, int value)
{
int low = 0;
int high = n;
while(low < high)
{
final int mid = (low + high)/2;
if(value >= a[mid])
low = mid + 1;
else
high = mid;
}
return low;
}
static int kthDiff(int a[], int n, int k)
{
Arrays.sort(a);
int low = a[1] - a[0];
for (int i = 1; i <= n-2; ++i)
low = Math.min(low, a[i+1] - a[i]);
int high = a[n-1] - a[0];
while (low < high)
{
int mid = (low + high) >> 1;
if (countPairs(a, n, mid) < k)
low = mid + 1;
else
high = mid;
}
return low;
}
public static void main(String args[])
{
Scanner s = new Scanner(System.in);
int k = 3;
int a[] = {1,2,3,4};
int n = a.length;
System.out.println(kthDiff(a, n, k));
}
}
|
Python3
from bisect import bisect as upper_bound
def countPairs(a, n, mid):
res = 0
for i in range(n):
res += upper_bound(a, a[i] + mid)
return res
def kthDiff(a, n, k):
a = sorted(a)
low = a[1] - a[0]
for i in range(1, n - 1):
low = min(low, a[i + 1] - a[i])
high = a[n - 1] - a[0]
while (low < high):
mid = (low + high) >> 1
if (countPairs(a, n, mid) < k):
low = mid + 1
else:
high = mid
return low
k = 3
a = [1, 2, 3, 4]
n = len(a)
print(kthDiff(a, n, k))
|
C#
using System;
class GFG{
static int countPairs(int[] a,
int n,
int mid)
{
int res = 0;
for(int i = 0; i < n; i++)
{
int ub = upperbound(a, n,
a[i] + mid);
res += (ub - (i));
}
return res;
}
static int upperbound(int []a,
int n,
int value)
{
int low = 0;
int high = n;
while(low < high)
{
int mid = (low + high)/2;
if(value >= a[mid])
low = mid + 1;
else
high = mid;
}
return low;
}
static int kthDiff(int []a,
int n, int k)
{
Array.Sort(a);
int low = a[1] - a[0];
for (int i = 1; i <= n - 2; ++i)
low = Math.Min(low, a[i + 1] -
a[i]);
int high = a[n - 1] - a[0];
while (low < high)
{
int mid = (low + high) >> 1;
if (countPairs(a, n, mid) < k)
low = mid + 1;
else
high = mid;
}
return low;
}
public static void Main(String []args)
{
int k = 3;
int []a = {1, 2, 3, 4};
int n = a.Length;
Console.WriteLine(kthDiff(a, n, k));
}
}
|
Javascript
<script>
function countPairs(a, n, mid) {
let res = 0;
for (let i = 0; i < n; i++) {
let ub = upperbound(a, n,
a[i] + mid);
res += (ub - (i));
}
return res;
}
function upperbound(a, n, value) {
let low = 0;
let high = n;
while (low < high) {
let mid = (low + high) / 2;
if (value >= a[mid])
low = mid + 1;
else
high = mid;
}
return low;
}
function kthDiff(a, n, k) {
a.sort((a, b) => a - b);
let low = a[1] - a[0];
for (let i = 1; i <= n - 2; ++i)
low = Math.min(low, a[i + 1] -
a[i]);
let high = a[n - 1] - a[0];
while (low < high) {
let mid = (low + high) >> 1;
if (countPairs(a, n, mid) < k)
low = mid + 1;
else
high = mid;
}
return low;
}
let k = 3;
let a = [1, 2, 3, 4];
let n = a.length;
document.write(kthDiff(a, n, k));
</script>
|
Time Complexity: O(nlogn)
Auxiliary Space: O(1)
Suppose, the maximum element in the array is, and the minimum element is a minimum element in the array is 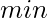 . Then time taken for the binary_search will be , and the time taken for the upper_bound function will be
. Then time taken for the binary_search will be , and the time taken for the upper_bound function will be 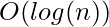
So, the time complexity of the algorithm is 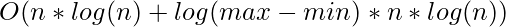 . Sorting takes
. Sorting takes 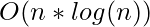 . After that the main binary search over low and high takes
. After that the main binary search over low and high takes 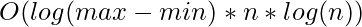 time because each call to the function countPairs takes time
time because each call to the function countPairs takes time 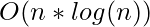 .
.
So the Overall time complexity would be 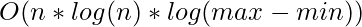
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...