Iterative Postorder Traversal | Set 1 (Using Two Stacks)
Last Updated :
11 Sep, 2023
We have discussed iterative inorder and iterative preorder traversals. In this post, iterative postorder traversal is discussed, which is more complex than the other two traversals (due to its nature of non-tail recursion, there is an extra statement after the final recursive call to itself). Postorder traversal can easily be done using two stacks, though. The idea is to push reverse postorder traversal to a stack. Once we have the reversed postorder traversal in a stack, we can just pop all items one by one from the stack and print them; this order of printing will be in postorder because of the LIFO property of stacks. Now the question is, how to get reversed postorder elements in a stack – the second stack is used for this purpose. For example, in the following tree, we need to get 1, 3, 7, 6, 2, 5, 4 in a stack. If we take a closer look at this sequence, we can observe that this sequence is very similar to the preorder traversal. The only difference is that the right child is visited before left child, and therefore the sequence is “root right left” instead of “root left right”. So, we can do something like iterative preorder traversal with the following differences:
a) Instead of printing an item, we push it to a stack.
b) We push the left subtree before the right subtree.
Following is the complete algorithm. After step 2, we get the reverse of a postorder traversal in the second stack. We use the first stack to get the correct order.
1. Push root to first stack.
2. Loop while first stack is not empty
2.1 Pop a node from first stack and push it to second stack
2.2 Push left and right children of the popped node to first stack
3. Print contents of second stack
Let us consider the following tree
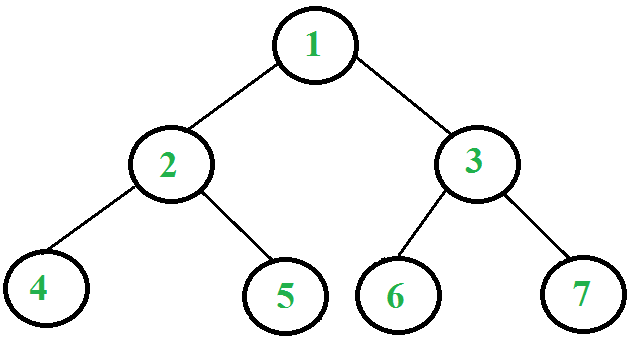
Following are the steps to print postorder traversal of the above tree using two stacks.
1. Push 1 to first stack.
First stack: 1
Second stack: Empty
2. Pop 1 from first stack and push it to second stack.
Push left and right children of 1 to first stack
First stack: 2, 3
Second stack: 1
3. Pop 3 from first stack and push it to second stack.
Push left and right children of 3 to first stack
First stack: 2, 6, 7
Second stack: 1, 3
4. Pop 7 from first stack and push it to second stack.
First stack: 2, 6
Second stack: 1, 3, 7
5. Pop 6 from first stack and push it to second stack.
First stack: 2
Second stack: 1, 3, 7, 6
6. Pop 2 from first stack and push it to second stack.
Push left and right children of 2 to first stack
First stack: 4, 5
Second stack: 1, 3, 7, 6, 2
7. Pop 5 from first stack and push it to second stack.
First stack: 4
Second stack: 1, 3, 7, 6, 2, 5
8. Pop 4 from first stack and push it to second stack.
First stack: Empty
Second stack: 1, 3, 7, 6, 2, 5, 4
The algorithm stops here since there are no more items in the first stack.
Observe that the contents of second stack are in postorder fashion. Print them.
Following is the implementation of iterative postorder traversal using two stacks.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
Node* newNode(int data)
{
Node* node = new Node;
node->data = data;
node->left = node->right = NULL;
return node;
}
void postOrderIterative(Node* root)
{
if (root == NULL)
return;
stack<Node *> s1, s2;
s1.push(root);
Node* node;
while (!s1.empty()) {
node = s1.top();
s1.pop();
s2.push(node);
if (node->left)
s1.push(node->left);
if (node->right)
s1.push(node->right);
}
while (!s2.empty()) {
node = s2.top();
s2.pop();
cout << node->data << " ";
}
}
int main()
{
Node* root = NULL;
root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
postOrderIterative(root);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100
struct Node {
int data;
struct Node *left, *right;
};
struct Stack {
int size;
int top;
struct Node** array;
};
struct Node* newNode(int data)
{
struct Node* node = (struct Node*)malloc(sizeof(struct Node));
node->data = data;
node->left = node->right = NULL;
return node;
}
struct Stack* createStack(int size)
{
struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
stack->size = size;
stack->top = -1;
stack->array = (struct Node**)malloc(stack->size * sizeof(struct Node*));
return stack;
}
int isFull(struct Stack* stack)
{
return stack->top - 1 == stack->size;
}
int isEmpty(struct Stack* stack)
{
return stack->top == -1;
}
void push(struct Stack* stack, struct Node* node)
{
if (isFull(stack))
return;
stack->array[++stack->top] = node;
}
struct Node* pop(struct Stack* stack)
{
if (isEmpty(stack))
return NULL;
return stack->array[stack->top--];
}
void postOrderIterative(struct Node* root)
{
if (root == NULL)
return;
struct Stack* s1 = createStack(MAX_SIZE);
struct Stack* s2 = createStack(MAX_SIZE);
push(s1, root);
struct Node* node;
while (!isEmpty(s1)) {
node = pop(s1);
push(s2, node);
if (node->left)
push(s1, node->left);
if (node->right)
push(s1, node->right);
}
while (!isEmpty(s2)) {
node = pop(s2);
printf("%d ", node->data);
}
}
int main()
{
struct Node* root = NULL;
root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
postOrderIterative(root);
return 0;
}
|
Java
import java.util.*;
public class IterativePostorder {
static class node {
int data;
node left, right;
public node(int data)
{
this.data = data;
}
}
static Stack<node> s1, s2;
static void postOrderIterative(node root)
{
s1 = new Stack<>();
s2 = new Stack<>();
if (root == null)
return;
s1.push(root);
while (!s1.isEmpty()) {
node temp = s1.pop();
s2.push(temp);
if (temp.left != null)
s1.push(temp.left);
if (temp.right != null)
s1.push(temp.right);
}
while (!s2.isEmpty()) {
node temp = s2.pop();
System.out.print(temp.data + " ");
}
}
public static void main(String[] args)
{
node root = null;
root = new node(1);
root.left = new node(2);
root.right = new node(3);
root.left.left = new node(4);
root.left.right = new node(5);
root.right.left = new node(6);
root.right.right = new node(7);
postOrderIterative(root);
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def postOrderIterative(root):
if root is None:
return
s1 = []
s2 = []
s1.append(root)
while s1:
node = s1.pop()
s2.append(node)
if node.left:
s1.append(node.left)
if node.right:
s1.append(node.right)
while s2:
node = s2.pop()
print(node.data,end=" ")
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.right.left = Node(6)
root.right.right = Node(7)
postOrderIterative(root)
|
C#
using System;
using System.Collections;
public class IterativePostorder {
public class node {
public int data;
public node left, right;
public node(int data)
{
this.data = data;
}
}
static public Stack s1, s2;
static void postOrderIterative(node root)
{
s1 = new Stack();
s2 = new Stack();
if (root == null)
return;
s1.Push(root);
while (s1.Count > 0) {
node temp = (node)s1.Pop();
s2.Push(temp);
if (temp.left != null)
s1.Push(temp.left);
if (temp.right != null)
s1.Push(temp.right);
}
while (s2.Count > 0) {
node temp = (node)s2.Pop();
Console.Write(temp.data + " ");
}
}
public static void Main(String[] args)
{
node root = null;
root = new node(1);
root.left = new node(2);
root.right = new node(3);
root.left.left = new node(4);
root.left.right = new node(5);
root.right.left = new node(6);
root.right.right = new node(7);
postOrderIterative(root);
}
}
|
Javascript
<script>
class node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
function postOrderIterative(root) {
var s1 = [];
var s2 = [];
if (root == null) return;
s1.push(root);
while (s1.length > 0) {
var temp = s1.pop();
s2.push(temp);
if (temp.left != null) s1.push(temp.left);
if (temp.right != null) s1.push(temp.right);
}
while (s2.length > 0) {
var temp = s2.pop();
document.write(temp.data + " ");
}
}
var root = null;
root = new node(1);
root.left = new node(2);
root.right = new node(3);
root.left.left = new node(4);
root.left.right = new node(5);
root.right.left = new node(6);
root.right.right = new node(7);
postOrderIterative(root);
</script>
|
Output:
4 5 2 6 7 3 1
Time complexity: O(n) where n is no of nodes in a binary tree
Auxiliary space: O(n) because using stack s1 and s2
Following is an overview of the above post.
Iterative preorder traversal can be easily implemented using two stacks. The first stack is used to get the reverse postorder traversal. The steps to get a reverse postorder are similar to iterative preorder.
You may also like to see a method which uses only one stack.
This article is compiled by Aashish Barnwal.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...