Convert Binary Tree to Doubly Linked List using inorder traversal
Last Updated :
05 Feb, 2024
Given a Binary Tree (Bt), convert it to a Doubly Linked List(DLL). The left and right pointers in nodes are to be used as previous and next pointers respectively in converted DLL. The order of nodes in DLL must be the same as in Inorder for the given Binary Tree. The first node of Inorder traversal (leftmost node in BT) must be the head node of the DLL.
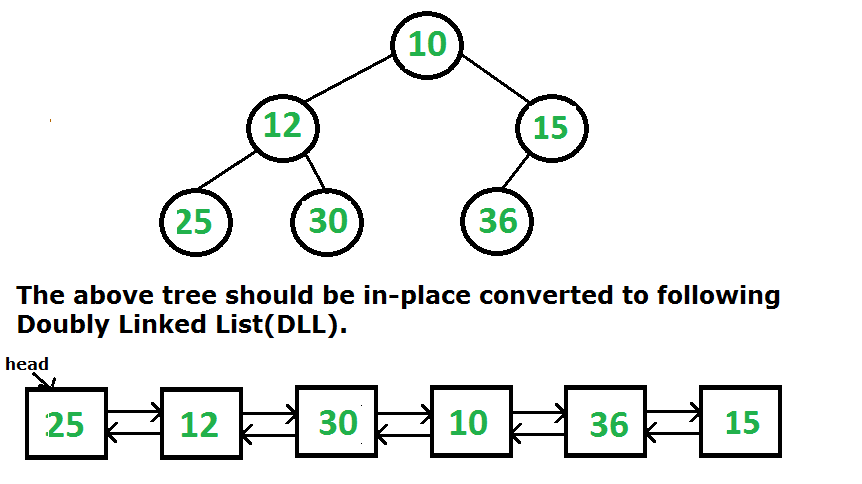
I came across this question during one of my interviews. A similar problem has been discussed in this post.
The problem here is simpler as we don’t need to create a circular DLL, but a simple DLL. The idea behind its solution is quite simple and straight.
- If the left subtree exists, process the left subtree
- Recursively convert the left subtree to DLL.
- Then find the inorder predecessor of the root in the left subtree (the inorder predecessor is the rightmost node in the left subtree).
- Make the inorder predecessor as the previous root and the root as the next in order predecessor.
- If the right subtree exists, process the right subtree (Below 3 steps are similar to the left subtree).
- Recursively convert the right subtree to DLL.
- Then find the inorder successor of the root in the right subtree (in order the successor is the leftmost node in the right subtree).
- Make the inorder successor as the next root and the root as the previous inorder successor.
- Find the leftmost node and return it (the leftmost node is always the head of a converted DLL).
Below is the source code for the above algorithm.
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public:
int data;
node* left;
node* right;
};
node* bintree2listUtil(node* root)
{
if (root == NULL)
return root;
if (root->left != NULL) {
node* left = bintree2listUtil(root->left);
for (; left->right != NULL; left = left->right)
;
left->right = root;
root->left = left;
}
if (root->right != NULL) {
node* right = bintree2listUtil(root->right);
for (; right->left != NULL; right = right->left)
;
right->left = root;
root->right = right;
}
return root;
}
node* bintree2list(node* root)
{
if (root == NULL)
return root;
root = bintree2listUtil(root);
while (root->left != NULL)
root = root->left;
return (root);
}
node* newNode(int data)
{
node* new_node = new node();
new_node->data = data;
new_node->left = new_node->right = NULL;
return (new_node);
}
void printList(node* node)
{
while (node != NULL) {
cout << node->data << " ";
node = node->right;
}
}
int main()
{
node* root = newNode(10);
root->left = newNode(12);
root->right = newNode(15);
root->left->left = newNode(25);
root->left->right = newNode(30);
root->right->left = newNode(36);
node* head = bintree2list(root);
printList(head);
return 0;
}
|
C
#include <stdio.h>
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* bintree2listUtil(struct node* root)
{
if (root == NULL)
return root;
if (root->left != NULL) {
struct node* left = bintree2listUtil(root->left);
for (; left->right != NULL; left = left->right)
;
left->right = root;
root->left = left;
}
if (root->right != NULL) {
struct node* right = bintree2listUtil(root->right);
for (; right->left != NULL; right = right->left)
;
right->left = root;
root->right = right;
}
return root;
}
struct node* bintree2list(struct node* root)
{
if (root == NULL)
return root;
root = bintree2listUtil(root);
while (root->left != NULL)
root = root->left;
return (root);
}
struct node* newNode(int data)
{
struct node* new_node
= (struct node*)malloc(sizeof(struct node));
new_node->data = data;
new_node->left = new_node->right = NULL;
return (new_node);
}
void printList(struct node* node)
{
while (node != NULL) {
printf("%d ", node->data);
node = node->right;
}
}
int main()
{
struct node* root = newNode(10);
root->left = newNode(12);
root->right = newNode(15);
root->left->left = newNode(25);
root->left->right = newNode(30);
root->right->left = newNode(36);
struct node* head = bintree2list(root);
printList(head);
return 0;
}
|
Java
class Node
{
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree
{
Node root;
Node bintree2listUtil(Node node)
{
if (node == null)
return node;
if (node.left != null)
{
Node left = bintree2listUtil(node.left);
for (; left.right != null; left = left.right);
left.right = node;
node.left = left;
}
if (node.right != null)
{
Node right = bintree2listUtil(node.right);
for (; right.left != null; right = right.left);
right.left = node;
node.right = right;
}
return node;
}
Node bintree2list(Node node)
{
if (node == null)
return node;
node = bintree2listUtil(node);
while (node.left != null)
node = node.left;
return node;
}
void printList(Node node)
{
while (node != null)
{
System.out.print(node.data + " ");
node = node.right;
}
}
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(12);
tree.root.right = new Node(15);
tree.root.left.left = new Node(25);
tree.root.left.right = new Node(30);
tree.root.right.left = new Node(36);
Node head = tree.bintree2list(tree.root);
tree.printList(head);
}
}
|
Python3
class Node(object):
def __init__(self, item):
self.data = item
self.left = None
self.right = None
def BTToDLLUtil(root):
if root is None:
return root
if root.left:
left = BTToDLLUtil(root.left)
while left.right:
left = left.right
left.right = root
root.left = left
if root.right:
right = BTToDLLUtil(root.right)
while right.left:
right = right.left
right.left = root
root.right = right
return root
def BTToDLL(root):
if root is None:
return root
root = BTToDLLUtil(root)
while root.left:
root = root.left
return root
def print_list(head):
if head is None:
return
while head:
print(head.data, end = " ")
head = head.right
if __name__ == '__main__':
root = Node(10)
root.left = Node(12)
root.right = Node(15)
root.left.left = Node(25)
root.left.right = Node(30)
root.right.left = Node(36)
head = BTToDLL(root)
print_list(head)
|
C#
using System;
public class Node
{
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree
{
public Node root;
public virtual Node bintree2listUtil(Node node)
{
if (node == null)
{
return node;
}
if (node.left != null)
{
Node left = bintree2listUtil(node.left);
for (; left.right != null; left = left.right)
{
;
}
left.right = node;
node.left = left;
}
if (node.right != null)
{
Node right = bintree2listUtil(node.right);
for (; right.left != null; right = right.left)
{
;
}
right.left = node;
node.right = right;
}
return node;
}
public virtual Node bintree2list(Node node)
{
if (node == null)
{
return node;
}
node = bintree2listUtil(node);
while (node.left != null)
{
node = node.left;
}
return node;
}
public virtual void printList(Node node)
{
while (node != null)
{
Console.Write(node.data + " ");
node = node.right;
}
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(12);
tree.root.right = new Node(15);
tree.root.left.left = new Node(25);
tree.root.left.right = new Node(30);
tree.root.right.left = new Node(36);
Node head = tree.bintree2list(tree.root);
tree.printList(head);
}
}
|
Javascript
<script>
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
var root;
function bintree2listUtil(node) {
if (node == null)
return node;
if (node.left != null) {
var left = bintree2listUtil(node.left);
for (; left.right != null; left = left.right)
left.right = node;
node.left = left;
}
if (node.right != null) {
var right = bintree2listUtil(node.right);
for (; right.left != null; right = right.left)
right.left = node;
node.right = right;
}
return node;
}
function bintree2list(node) {
if (node == null)
return node;
node = bintree2listUtil(node);
while (node.left != null)
node = node.left;
return node;
}
function printList(node) {
while (node != null) {
document.write(node.data + " ");
node = node.right;
}
}
root = new Node(10);
root.left = new Node(12);
root.right = new Node(15);
root.left.left = new Node(25);
root.left.right = new Node(30);
root.right.left = new Node(36);
var head = bintree2list(root);
printList(head);
</script>
|
Time Complexity: O(n).
Auxiliary Space: O(1).
Another Approach:
Algorithm:
- Traverse the tree in inorder fashion.
- While visiting each node, keep track of DLL’s head and tail pointers, insert each visited node to the end of DLL using tail pointer.
- Return head of the list.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public:
int data;
node* left;
node* right;
};
void bintree2listUtil(node* root, node** head, node** tail)
{
if (root == NULL)
return;
bintree2listUtil(root->left, head, tail);
if (*head == NULL) {
*head = root;
}
root->left = *tail;
if (*tail != NULL) {
(*tail)->right = root;
}
*tail = root;
bintree2listUtil(root->right, head, tail);
}
node* bintree2list(node* root)
{
if (root == NULL)
return root;
node* head = NULL;
node* tail = NULL;
bintree2listUtil(root, &head, &tail);
return head;
}
node* newNode(int data)
{
node* new_node = new node();
new_node->data = data;
new_node->left = new_node->right = NULL;
return (new_node);
}
void printList(node* node)
{
while (node != NULL) {
cout << node->data << " ";
node = node->right;
}
}
int main()
{
node* root = newNode(10);
root->left = newNode(12);
root->right = newNode(15);
root->left->left = newNode(25);
root->left->right = newNode(30);
root->right->left = newNode(36);
node* head = bintree2list(root);
printList(head);
return 0;
}
|
Java
import java.util.*;
public class GFG {
static class node {
int data;
node left;
node right;
};
static node head, tail;
static void bintree2listUtil(node root)
{
if (root == null)
return;
node left = root.left;
node right = root.right;
bintree2listUtil(root.left);
if (head == null) {
head = root;
}
root.left = tail;
if (tail != null) {
(tail).right = root;
}
tail = root;
bintree2listUtil(root.right);
}
static void bintree2list(node root)
{
if (root == null)
head = root;
bintree2listUtil(root);
}
static node newNode(int data)
{
node new_node = new node();
new_node.data = data;
new_node.left = new_node.right = null;
return (new_node);
}
static void printList()
{
while (head != null) {
System.out.print(head.data + " ");
head = head.right;
}
}
public static void main(String[] args)
{
node root = newNode(10);
root.left = newNode(12);
root.right = newNode(15);
root.left.left = newNode(25);
root.left.right = newNode(30);
root.right.left = newNode(36);
head = null;
tail = null;
bintree2list(root);
printList();
}
}
|
Python3
class newNode(object):
def __init__(self,data):
self.data = data
self.left = None
self.right = None
head = None
tail = None
def bintree2listUtil(root):
if (root == None):
return
left = root.left
right = root.right
global head
global tail
bintree2listUtil(root.left)
if (head == None):
head = root
root.left = tail
if (tail != None):
tail.right = root
tail = root
bintree2listUtil(root.right)
def bintree2list(root):
global head
if (root == None):
head = root
bintree2listUtil(root)
def printList():
global head
while head:
print(head.data, end = " ")
head = head.right
if __name__ == '__main__':
root = newNode(10)
root.left = newNode(12)
root.right = newNode(15)
root.left.left = newNode(25)
root.left.right = newNode(30)
root.right.left = newNode(36)
bintree2list(root)
printList()
|
C#
using System;
public class GFG {
public class node {
public int data;
public node left;
public node right;
};
static node head, tail;
static void bintree2listUtil(node root) {
if (root == null)
return;
node left = root.left;
node right = root.right;
bintree2listUtil(root.left);
if (head == null) {
head = root;
}
root.left = tail;
if (tail != null) {
(tail).right = root;
}
tail = root;
bintree2listUtil(root.right);
}
static void bintree2list(node root) {
if (root == null)
head = root;
bintree2listUtil(root);
}
static node newNode(int data) {
node new_node = new node();
new_node.data = data;
new_node.left = new_node.right = null;
return (new_node);
}
static void printList() {
while (head != null) {
Console.Write(head.data + " ");
head = head.right;
}
}
public static void Main(String[] args) {
node root = newNode(10);
root.left = newNode(12);
root.right = newNode(15);
root.left.left = newNode(25);
root.left.right = newNode(30);
root.right.left = newNode(36);
head = null;
tail = null;
bintree2list(root);
printList();
}
}
|
Javascript
<script>
class Node {
constructor() {
this.data = 0;
this.left = null;
this.right = null;
}
}
var head, tail;
function bintree2listUtil(root) {
if (root == null)
return;
var left = root.left;
var right = root.right;
bintree2listUtil(root.left);
if (head == null) {
head = root;
}
root.left = tail;
if (tail != null) {
(tail).right = root;
}
tail = root;
bintree2listUtil(root.right);
}
function bintree2list( root) {
if (root == null)
head = root;
bintree2listUtil(root);
}
function newNode(data) {
var new_node = new Node();
new_node.data = data;
new_node.left = new_node.right = null;
return (new_node);
}
function printList() {
while (head != null) {
document.write(head.data + " ");
head = head.right;
}
}
var root = newNode(10);
root.left = newNode(12);
root.right = newNode(15);
root.left.left = newNode(25);
root.left.right = newNode(30);
root.right.left = newNode(36);
head = null;
tail = null;
bintree2list(root);
printList();
</script>
|
Time Complexity: O(n) where n is the number of nodes in given Binary Tree.
Auxiliary Space: O(h) where h is the height of given Binary Tree due to Recursion
This article is compiled by Ashish Mangla and reviewed by GeeksforGeeks team.
You may also like to see Convert a given Binary Tree to Doubly Linked List | Set 2 for another simple and efficient solution.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...