A height balanced binary tree is a binary tree in which the height of the left subtree and right subtree of any node does not differ by more than 1 and both the left and right subtree are also height balanced.
In this article, we will look into methods how to determine if given Binary trees are height-balanced
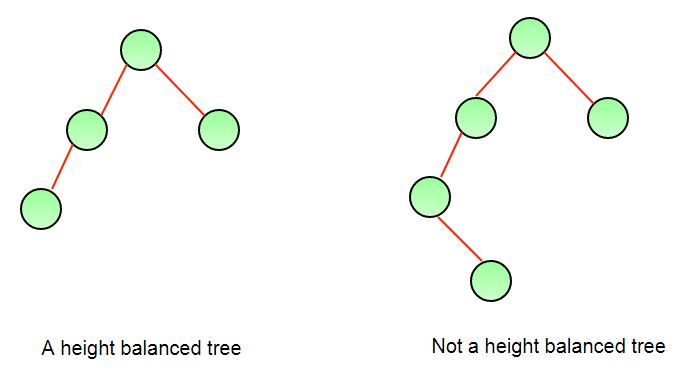
Examples: The tree on the left is a height balanced binary tree. Whereas the tree on the right is not a height balanced tree. Because the left subtree of the root has a height which is 2 more than the height of the right subtree.
Naive Approach: To check if a tree is height-balanced:
Get the height of left and right subtrees using dfs traversal. Return true if the difference between heights is not more than 1 and left and right subtrees are balanced, otherwise return false.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int d)
{
int data = d;
left = right = NULL;
}
};
int height(Node* node)
{
if (node == NULL)
return 0;
return 1 + max(height(node->left), height(node->right));
}
bool isBalanced(Node* root)
{
int lh;
int rh;
if (root == NULL)
return 1;
lh = height(root->left);
rh = height(root->right);
if (abs(lh - rh) <= 1 && isBalanced(root->left)
&& isBalanced(root->right))
return 1;
return 0;
}
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->left->left->left = new Node(8);
if (isBalanced(root))
cout << "Tree is balanced";
else
cout << "Tree is not balanced";
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
#define bool int
struct node {
int data;
struct node* left;
struct node* right;
};
int height(struct node* node);
bool isBalanced(struct node* root)
{
int lh;
int rh;
if (root == NULL)
return 1;
lh = height(root->left);
rh = height(root->right);
if (abs(lh - rh) <= 1 && isBalanced(root->left)
&& isBalanced(root->right))
return 1;
return 0;
}
int max(int a, int b) { return (a >= b) ? a : b; }
int height(struct node* node)
{
if (node == NULL)
return 0;
return 1 + max(height(node->left), height(node->right));
}
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->left->left->left = newNode(8);
if (isBalanced(root))
printf("Tree is balanced");
else
printf("Tree is not balanced");
getchar();
return 0;
}
|
Java
class Node {
int data;
Node left, right;
Node(int d)
{
data = d;
left = right = null;
}
}
class BinaryTree {
Node root;
boolean isBalanced(Node node)
{
int lh;
int rh;
if (node == null)
return true;
lh = height(node.left);
rh = height(node.right);
if (Math.abs(lh - rh) <= 1 && isBalanced(node.left)
&& isBalanced(node.right))
return true;
return false;
}
int height(Node node)
{
if (node == null)
return 0;
return 1
+ Math.max(height(node.left),
height(node.right));
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.left.left.left = new Node(8);
if (tree.isBalanced(tree.root))
System.out.println("Tree is balanced");
else
System.out.println("Tree is not balanced");
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def height(root):
if root is None:
return 0
return max(height(root.left), height(root.right)) + 1
def isBalanced(root):
if root is None:
return True
lh = height(root.left)
rh = height(root.right)
if (abs(lh - rh) <= 1) and isBalanced(
root.left) is True and isBalanced(root.right) is True:
return True
return False
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.left.left.left = Node(8)
if isBalanced(root):
print("Tree is balanced")
else:
print("Tree is not balanced")
|
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int d)
{
data = d;
left = right = null;
}
}
public class BinaryTree {
public Node root;
public virtual bool isBalanced(Node node)
{
int lh;
int rh;
if (node == null) {
return true;
}
lh = height(node.left);
rh = height(node.right);
if (Math.Abs(lh - rh) <= 1 && isBalanced(node.left)
&& isBalanced(node.right)) {
return true;
}
return false;
}
public virtual int height(Node node)
{
if (node == null) {
return 0;
}
return 1
+ Math.Max(height(node.left),
height(node.right));
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.left.left.left = new Node(8);
if (tree.isBalanced(tree.root)) {
Console.WriteLine("Tree is balanced");
}
else {
Console.WriteLine("Tree is not balanced");
}
}
}
|
Javascript
<script>
class Node{
constructor(data){
this.data = data
this.left = null
this.right = null
}
}
function height(root){
if(root == null)
return 0
return Math.max(height(root.left), height(root.right)) + 1
}
function isBalanced(root){
if(root == null)
return true
let lh = height(root.left)
let rh = height(root.right)
if (Math.abs(lh - rh) <= 1 && isBalanced(
root.left)== true && isBalanced( root.right) == true)
return true
return false
}
let root = new Node(1)
root.left = new Node(2)
root.right = new Node(3)
root.left.left = new Node(4)
root.left.right = new Node(5)
root.left.left.left = new Node(8)
if(isBalanced(root))
document.write("Tree is balanced","</br>")
else
document.write("Tree is not balanced","</br>")
</script>
|
OutputTree is not balanced
Time Complexity: O(n^2) in case of full binary tree.
Auxiliary Space: O(n) space for call stack since using recursion
Efficient implementation: Above implementation can be optimized by
Calculating the height in the same recursion rather than calling a height() function separately.
- For each node make two recursion calls – one for left subtree and the other for the right subtree.
- Based on the heights returned from the recursion calls, decide if the subtree whose root is the current node is height-balanced or not.
- If it is balanced then return the height of that subtree. Otherwise, return -1 to denote that the subtree is not height-balanced.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node* left;
struct Node* right;
Node(int k)
{
key = k;
left = right = NULL;
}
};
int isBalanced(Node* root)
{
if (root == NULL)
return 0;
int lh = isBalanced(root->left);
if (lh == -1)
return -1;
int rh = isBalanced(root->right);
if (rh == -1)
return -1;
if (abs(lh - rh) > 1)
return -1;
else
return max(lh, rh) + 1;
}
int main()
{
Node* root = new Node(10);
root->left = new Node(5);
root->right = new Node(30);
root->right->left = new Node(15);
root->right->right = new Node(20);
if (isBalanced(root) > 0)
cout << "Balanced";
else
cout << "Not Balanced";
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
#define bool int
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int isBalanced(struct node* root)
{
if (root == NULL)
return 0;
int lh = isBalanced(root->left);
if (lh == -1)
return -1;
int rh = isBalanced(root->right);
if (rh == -1)
return -1;
if (abs(lh - rh) > 1)
return -1;
else
return lh > rh ? lh + 1 : rh + 1;
}
int main()
{
int height = 0;
struct node* root = newNode(10);
root->left = newNode(5);
root->right = newNode(30);
root->right->left = newNode(15);
root->right->right = newNode(20);
if (isBalanced(root) > 0)
printf("Balanced");
else
printf("Not Balanced");
getchar();
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
class Node {
int key;
Node left;
Node right;
Node(int k)
{
key = k;
left = right = null;
}
}
class GFG {
public static void main(String args[])
{
Node root = new Node(10);
root.left = new Node(5);
root.right = new Node(30);
root.right.left = new Node(15);
root.right.right = new Node(20);
if (isBalanced(root) > 0)
System.out.print("Balanced");
else
System.out.print("Not Balanced");
}
public static int isBalanced(Node root)
{
if (root == null)
return 0;
int lh = isBalanced(root.left);
if (lh == -1)
return -1;
int rh = isBalanced(root.right);
if (rh == -1)
return -1;
if (Math.abs(lh - rh) > 1)
return -1;
else
return Math.max(lh, rh) + 1;
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def isBalanced(root):
if root is None:
return True
lh = isBalanced(root.left)
if lh == 0:
return 0
rh = isBalanced(root.right)
if rh == 0:
return 0
if (abs(lh - rh) > 1):
return 0
else:
return max(lh, rh) + 1
if __name__ == '__main__':
root = Node(10)
root.left = Node(5)
root.right = Node(30)
root.right.left = Node(15)
root.right.right = Node(20)
if (isBalanced(root) == 0):
print("Not Balanced")
else:
print("Balanced")
|
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int d)
{
data = d;
left = right = null;
}
}
public class BinaryTree {
public Node root;
public virtual int isBalanced(Node root)
{
if (root == null)
return 0;
int lh = isBalanced(root.left);
if (lh == -1)
return -1;
int rh = isBalanced(root.right);
if (rh == -1)
return -1;
if (lh > rh + 1 || rh > lh + 1)
return -1;
else
return Math.Max(lh, rh) + 1;
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(10);
tree.root.left = new Node(5);
tree.root.right = new Node(30);
tree.root.right.left = new Node(15);
tree.root.right.right = new Node(20);
if (tree.isBalanced(tree.root) > 0) {
Console.WriteLine("Balanced");
}
else {
Console.WriteLine("Not Balanced");
}
}
}
|
Javascript
<script>
class Node{
constructor(data){
this.data = data
this.left = this.right = null
}
}
function isBalanced(root)
{
if (root == null)
return 0;
int lh = isBalanced(root.left);
if (lh == -1)
return -1;
int rh = isBalanced(root.right);
if (rh == -1)
return -1;
if (Math.abs(lh - rh) > 1)
return -1;
else
return Math.max(lh, rh) + 1;
}
let root = new Node(10)
root.left = new Node(5)
root.right = new Node(30)
root.right.left = new Node(15)
root.right.right = new Node(20)
if(isBalanced(root) > 0)
document.write('Balanced',"</br>")
else
document.write('Not Balanced',"</br>")
</script>
|
Time Complexity: O(n)
- Because we are only one dfs call and utilizing the height returned from that to determine the height balance, it is performing the task in linear time.
Auxiliary Space: O(n)
Using Pair:
The idea is simple instead of calling two recursive function ‘isBalanced’ and ‘height’ we can use a pair in which first value will represent that if any subtree is balanced or not and second value will represent the height of the every subtree in this way we can easily find that if tree is balanced or not.
Follow the steps below to implement the above idea:
- Define a helper function isBalancedfast that takes a root node as input and returns a pair of boolean and integer values representing whether the tree rooted at the given node is balanced and its height, respectively.
- Define the base case for the recursion: if the root node is NULL, return a pair with first set to true and second set to 0.
- Recursively call isBalancedfast on the left and right subtrees of the current node.
- Retrieve the boolean and integer values from the returned pairs and set them to leftAns, rightAns, leftHeight, and rightHeight.
- Calculate the height of the current node by taking the maximum height of its left and right subtrees and adding 1.
- Check if the absolute difference between the heights of the left and right subtrees is less than or equal to 1. If so, set diff to true; otherwise, set it to false.
- Set ans.first to true if leftAns, rightAns, and diff are all true; otherwise, set it to false.
- Set ans.second to the height of the current node.
- Return ans.
- Define a public function isBalanced that takes a root node as input and calls the isBalancedfast helper function on the root node.
- Return the first element of the pair returned by the isBalancedfast function. This represents whether the entire binary tree is balanced or not.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int val;
Node *left, *right;
Node(int v)
: val(v)
, left(nullptr)
, right(nullptr)
{
}
};
class Solution {
pair<bool, int> isBalancedfast(Node* root)
{
if (root == NULL) {
pair<bool, int> p = make_pair(true, 0);
return p;
}
pair<int, int> left = isBalancedfast(root->left);
pair<int, int> right = isBalancedfast(root->right);
bool leftAns = left.first;
bool rightAns = right.first;
bool diff = abs(left.second - right.second) <= 1;
pair<bool, int> ans;
ans.second = max(left.second, right.second) + 1;
if (leftAns && rightAns && diff) {
ans.first = true;
}
else {
ans.first = false;
}
return ans;
}
public:
bool isBalanced(Node* root)
{
return isBalancedfast(root).first;
}
};
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->left->left->left = new Node(8);
Solution obj;
if (obj.isBalanced(root)) {
cout << "The given binary tree is balanced."
<< endl;
}
else {
cout << "The given binary tree is not balanced."
<< endl;
}
return 0;
}
|
C#
using System;
public class Node {
public int val;
public Node left;
public Node right;
public Node(int v)
{
val = v;
left = null;
right = null;
}
}
public class Solution {
public(bool, int) IsBalancedfast(Node root)
{
if (root == null) {
return (true, 0);
}
var left = IsBalancedfast(root.left);
var right = IsBalancedfast(root.right);
bool leftAns = left.Item1;
bool rightAns = right.Item1;
bool diff = Math.Abs(left.Item2 - right.Item2) <= 1;
if (leftAns && rightAns && diff) {
return (true,
Math.Max(left.Item2, right.Item2) + 1);
}
else {
return (false, 0);
}
}
public bool IsBalanced(Node root)
{
return IsBalancedfast(root).Item1;
}
}
public class Program {
public static void Main(string[] args)
{
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.left.left.left = new Node(8);
Solution obj = new Solution();
if (obj.IsBalanced(root)) {
Console.WriteLine(
"The given binary tree is balanced.");
}
else {
Console.WriteLine(
"The given binary tree is not balanced.");
}
}
}
|
Java
class Node {
int val;
Node left, right;
public Node(int v) {
val = v;
left = null;
right = null;
}
}
class Solution {
private Pair<Boolean, Integer> isBalancedfast(Node root) {
if (root == null) {
Pair<Boolean, Integer> p = new Pair<>(true, 0);
return p;
}
Pair<Boolean, Integer> left = isBalancedfast(root.left);
Pair<Boolean, Integer> right = isBalancedfast(root.right);
boolean leftAns = left.first;
boolean rightAns = right.first;
boolean diff = Math.abs(left.second - right.second) <= 1;
Pair<Boolean, Integer> ans = new Pair<>(false, Math.max(left.second, right.second) + 1);
if (leftAns && rightAns && diff) {
ans = new Pair<>(true, Math.max(left.second, right.second) + 1);
}
return ans;
}
public boolean isBalanced(Node root) {
return isBalancedfast(root).first;
}
}
public class Main {
public static void main(String[] args) {
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.left.left.left = new Node(8);
Solution obj = new Solution();
if (obj.isBalanced(root)) {
System.out.println("The given binary tree is balanced.");
} else {
System.out.println("The given binary tree is not balanced.");
}
}
}
|
Python3
class Node:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class Solution:
def isBalancedfast(self, root):
if root is None:
return True, 0
left = self.isBalancedfast(root.left)
right = self.isBalancedfast(root.right)
leftAns = left[0]
rightAns = right[0]
diff = abs(left[1] - right[1]) <= 1
height = max(left[1], right[1]) + 1
if leftAns and rightAns and diff:
return True, height
else:
return False, height
def isBalanced(self, root):
return self.isBalancedfast(root)[0]
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
root.left.left.left = Node(8)
obj = Solution()
if obj.isBalanced(root):
print("The given binary tree is balanced.")
else:
print("The given binary tree is not balanced.")
|
Javascript
class Node {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class Solution
{
isBalancedfast(root)
{
if (root == null) {
return [true, 0];
}
let left = this.isBalancedfast(root.left);
let right = this.isBalancedfast(root.right);
let leftAns = left[0];
let rightAns = right[0];
let diff = Math.abs(left[1] - right[1]) <= 1;
let ans = [];
ans[1] = Math.max(left[1], right[1]) + 1;
if (leftAns && rightAns && diff) {
ans[0] = true;
}
else {
ans[0] = false;
}
return ans;
}
isBalanced(root) {
return this.isBalancedfast(root)[0];
}
}
let root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.left.left.left = new Node(8);
let obj = new Solution();
if (obj.isBalanced(root)) {
console.log("The given binary tree is balanced.");
}
else {
console.log("The given binary tree is not balanced.");
}
|
OutputThe given binary tree is not balanced.
Time Complexity: O(N) , where N is the number of nodes present in the tree, This is Because every node of the tree is visited only ones.
Auxiliary Space: O(H) , where h is the height of the binary tree.
Asked in: Amazon, Belzabar, Goldman Sachs, InMobi, Intel, Microsoft, Paytm, Synopsys, Walmart, Zillious
Please write comments if you find any of the above codes/algorithms incorrect, or find other ways to solve the same problem.