Graph and its representations
Last Updated :
02 Jan, 2024
What is Graph Data Structure?
A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(V, E).
Representations of Graph
Here are the two most common ways to represent a graph :
- Adjacency Matrix
- Adjacency List
An adjacency matrix is a way of representing a graph as a matrix of boolean (0’s and 1’s).
Let’s assume there are n vertices in the graph So, create a 2D matrix adjMat[n][n] having dimension n x n.
- If there is an edge from vertex i to j, mark adjMat[i][j] as 1.
- If there is no edge from vertex i to j, mark adjMat[i][j] as 0.
Representation of Undirected Graph to Adjacency Matrix:
The below figure shows an undirected graph. Initially, the entire Matrix is initialized to 0. If there is an edge from source to destination, we insert 1 to both cases (adjMat[destination] and adjMat[destination]) because we can go either way.
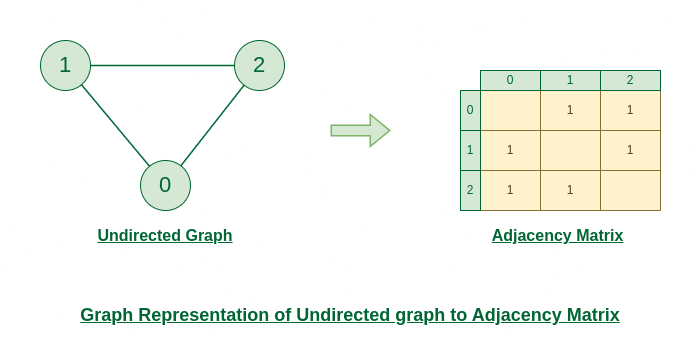
Undirected Graph to Adjacency Matrix
Representation of Directed Graph to Adjacency Matrix:
The below figure shows a directed graph. Initially, the entire Matrix is initialized to 0. If there is an edge from source to destination, we insert 1 for that particular adjMat[destination].
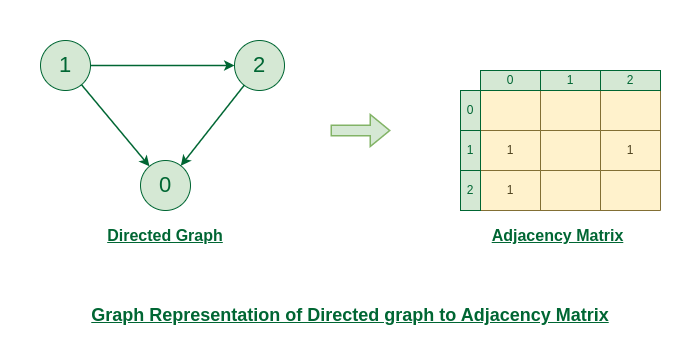
Directed Graph to Adjacency Matrix
An array of Lists is used to store edges between two vertices. The size of array is equal to the number of vertices (i.e, n). Each index in this array represents a specific vertex in the graph. The entry at the index i of the array contains a linked list containing the vertices that are adjacent to vertex i.
Let’s assume there are n vertices in the graph So, create an array of list of size n as adjList[n].
- adjList[0] will have all the nodes which are connected (neighbour) to vertex 0.
- adjList[1] will have all the nodes which are connected (neighbour) to vertex 1 and so on.
Representation of Undirected Graph to Adjacency list:
The below undirected graph has 3 vertices. So, an array of list will be created of size 3, where each indices represent the vertices. Now, vertex 0 has two neighbours (i.e, 1 and 2). So, insert vertex 1 and 2 at indices 0 of array. Similarly, For vertex 1, it has two neighbour (i.e, 2 and 0) So, insert vertices 2 and 0 at indices 1 of array. Similarly, for vertex 2, insert its neighbours in array of list.
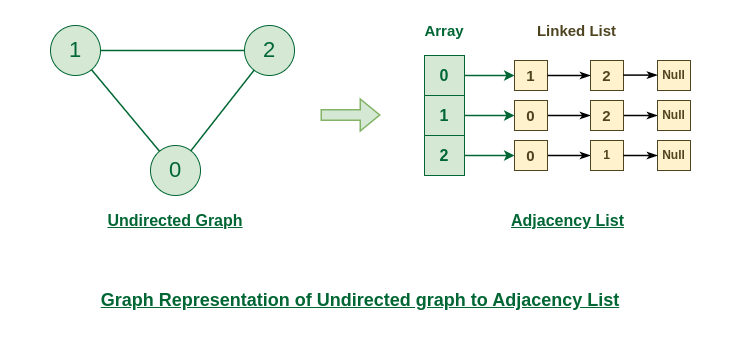
Undirected Graph to Adjacency list
Representation of Directed Graph to Adjacency list:
The below directed graph has 3 vertices. So, an array of list will be created of size 3, where each indices represent the vertices. Now, vertex 0 has no neighbours. For vertex 1, it has two neighbour (i.e, 0 and 2) So, insert vertices 0 and 2 at indices 1 of array. Similarly, for vertex 2, insert its neighbours in array of list.
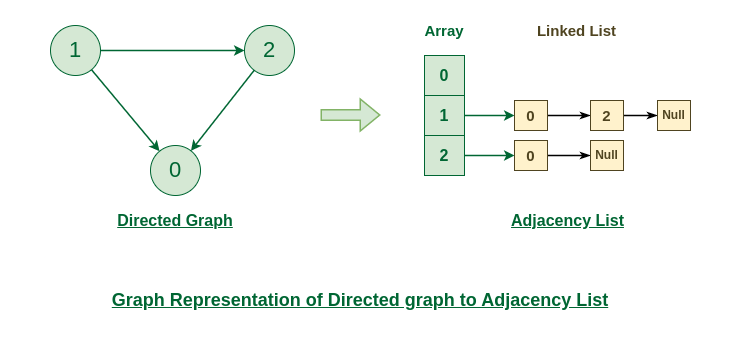
Directed Graph to Adjacency list
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...