Given a large number, check if a subsequence of digits is divisible by 8

Given a number of at most 100 digits. We have to check if it is possible, after removing certain digits, to obtain a number of at least one digit which is divisible by 8. We are forbidden to rearrange the digits.

Examples :

Input : 1787075866
Output : Yes
There exist more one or more subsequences
divisible by 8. Example subsequences are
176, 16 and 8.

Input : 6673177113
Output : No 
No subsequence is divisible by 8.

Input : 3144
Output : Yes
The subsequence 344 is divisible by 8.

Property of the divisibility by eight: number can be divided by eight if and only if its last three digits form a number that can be divided by eight. Thus, it is enough to test only numbers that can be obtained from the original one by crossing out and that contain at most three digits i.e we check all one-digit, two digits, and three-digit number combinations.

Method 1 (Brute Force):
We apply the brute force approach. We permute all possible single-digit, double-digit, and triple-digit combinations using an iterative ladder. If we encounter a single-digit number divisible by 8 or a double-digit number combination divisible by 8 or a triple-digit number combination divisible by 8, then that will be the solution to our problem.

C++

// C++ program to check if a subsequence of digits
// is divisible by 8.
#include <bits/stdc++.h>
using namespace std;

// Function to calculate any permutation divisible
// by 8. If such permutation exists, the function
// will return that permutation else it will return -1
bool isSubSeqDivisible(string str)
{
    // Converting string to integer array for ease
    // of computations (Indexing in arr[] is
    // considered to be starting from 1)
    int l = str.length();
    int arr[l];
    for (int i = 0; i < l; i++)
        arr[i] = str[i] - '0';

    // Generating all possible permutations and checking
    // if any such permutation is divisible by 8
    for (int i = 0; i < l; i++) {
        for (int j = i; j < l; j++) {
            for (int k = j; k < l; k++) {
                if (arr[i] % 8 == 0)
                    return true;

                else if ((arr[i] * 10 + arr[j]) % 8 == 0 && i != j)
                    return true;

                else if ((arr[i] * 100 + arr[j] * 10 + arr[k]) % 8 == 0 && i != j && j != k && i != k)
                    return true;
            }
        }
    }
    return false;
}

// Driver function
int main()
{
    string str = "3144";
    if (isSubSeqDivisible(str))
        cout << "Yes";
    else
        cout << "No";
    return 0;
}

Java

// Java program to check if a subsequence
// of digits is divisible by 8.
import java.io.*;

class GFG {

    // Function to calculate any permutation
    // divisible by 8. If such permutation
    // exists, the function will return
    // that permutation else it will return -1
    static boolean isSubSeqDivisible(String str)
    {

        int i, j, k, l = str.length();
        int arr[] = new int[l];

        // Converting string to integer array for ease
        // of computations (Indexing in arr[] is
        // considered to be starting from 1)
        for (i = 0; i < l; i++)
            arr[i] = str.charAt(i) - '0';

        // Generating all possible permutations
        // and checking if any such
        // permutation is divisible by 8
        for (i = 0; i < l; i++) {
            for (j = i; j < l; j++) {
                for (k = j; k < l; k++) {
                    if (arr[i] % 8 == 0)
                        return true;

                    else if ((arr[i] * 10 + arr[j]) % 8 == 0 && i != j)
                        return true;

                    else if ((arr[i] * 100 + arr[j] * 10 + arr[k]) % 8 == 0
                             && i != j && j != k && i != k)
                        return true;
                }
            }
        }
        return false;
    }

    // Driver function
    public static void main(String args[])
    {

        String str = "3144";
        if (isSubSeqDivisible(str))
            System.out.println("Yes");
        else
            System.out.println("No");
    }
}

// This code is contributed by Nikita Tiwari.

Python3

# Python3 program to
# check if a subsequence of digits
# is divisible by 8.

# Function to calculate any
# permutation divisible
# by 8. If such permutation
# exists, the function
# will return that permutation
# else it will return -1
def isSubSeqDivisible(st) :

    l = len(st)
    arr = [int(ch) for ch in st]

    # Generating all possible
    # permutations and checking
    # if any such permutation
    # is divisible by 8
    for i in range(0, l) :
        for j in range(i, l) :
            for k in range(j, l) :
                if (arr[i] % 8 == 0) :
                    return True

                elif ((arr[i]*10 + arr[j])% 8 == 0 and i != j) :
                    return True

                elif ((arr[i] * 100 + arr[j] * 10 + arr[k]) % 8 == 0 and i != j and j != k and i != k) :
                    return True

    return False

# Driver function

st = "3144"
if (isSubSeqDivisible(st)) :
    print("Yes")
else :
    print("No")

# This code is contributed
# by Nikita Tiwari.

C#

// C# program to check if a subsequence
// of digits is divisible by 8.
using System;

class GFG {

    // Function to calculate any permutation
    // divisible by 8. If such permutation
    // exists, the function will return
    // that permutation else it will return -1
    static bool isSubSeqDivisible(string str)
    {
        int i, j, k, l = str.Length;
        int[] arr = new int[l];

        // Converting string to integer array for ease
        // of computations (Indexing in arr[] is
        // considered to be starting from 1)
        for (i = 0; i < n; i++)
           arr[i] = str[i] - '0';

        // Generating all possible permutations
        // and checking if any such
        // permutation is divisible by 8
        for (i = 0; i < l; i++) {
            for (j = i; j < l; j++) {
                for (k = j; k < l; k++) {
                    if (arr[i] % 8 == 0)
                        return true;

                    else if ((arr[i] * 10 + arr[j])
                                     % 8
                                 == 0
                             && i != j)
                        return true;

                    else if ((arr[i] * 100 + arr[j] * 10 + arr[k]) % 8 == 0
                             && i != j && j != k
                             && i != k)
                        return true;
                }
            }
        }

        return false;
    }

    // Driver function
    public static void Main()
    {
        string str = "3144";

        if (isSubSeqDivisible(str))
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");
    }
}

// This code is contributed by vt_m.

Javascript

<script>

// JavaScript program to check if a subsequence
// of digits is divisible by 8.

// Function to calculate any permutation
// divisible by 8. If such permutation
// exists, the function will return
// that permutation else it will return -1
function isSubSeqDivisible(str)
{
    let i, j, k, l = str.length;
    let arr = [];

    // Converting string to integer array for ease
    // of computations (Indexing in arr[] is
    // considered to be starting from 1)
    for(i = 0; i < l; i++)
       arr[i] = str[i] - '0';

    // Generating all possible permutations
    // and checking if any such
    // permutation is divisible by 8
    for(i = 0; i < l; i++)
    {
        for(j = i; j < l; j++)
        {
            for(k = j; k < l; k++)
            {
                if (arr[i] % 8 == 0)
                    return true;

                else if ((arr[i] * 10 + arr[j]) %
                               8 == 0 && i != j)
                    return true;

                else if ((arr[i] * 100 + arr[j] * 10 +
                         arr[k]) % 8 == 0 && i != j &&
                              j != k && i != k)
                    return true;
            }
        }
    }
    return false;
}

// Driver Code
let str = "3144";
if (isSubSeqDivisible(str))
    document.write("Yes");
else
    document.write("No");

// This code is contributed by susmitakundugoaldanga

</script>

PHP

<?php


  // PHP program to check if a subsequence
// of digits is divisible by 8.

// Function to calculate any permutation
// divisible by 8. If such permutation
// exists, the function will return
// that permutation else it will return -1
function isSubSeqDivisible($str)
{
    $l = strlen($str);
    $arr = [];

    // Converting string to integer array for ease
    // of computations (Indexing in arr[] is
    // considered to be starting from 1)
    for($i = 0; $i < $l; $i++)
       $arr[$i] = $str[$i] - '0';

    // Generating all possible permutations
    // and checking if any such
    // permutation is divisible by 8
    for($i = 0; $i < $l; $i++)
    {
        for($j = $i; $j < $l; $j++)
        {
            for($k = $j; $k < $l; $k++)
            {
                if ($arr[$i] % 8 == 0)
                    return true;

                else if (($arr[$i] * 10 + $arr[$j]) %
                               8 == 0 && $i != $j)
                    return true;

                else if (($arr[$i] * 100 + $arr[$j] * 10 +
                         $arr[$k]) % 8 == 0 && $i != $j &&
                              $j != $k && $i != $k)
                    return true;
            }
        }
    }
    return false;
}

// Driver Code
$str = "3144";
if (isSubSeqDivisible($str))
    echo("Yes");
else
    echo("No");



?>
// THIS CODE IS CONTRIBUTED BY GANGARAJULA LAXMI

Output

Yes

Time Complexity: O(N³), as we are using nested loops for traversing N³ times. Where N is the length of the string.

Auxiliary Space: O(N), as we are using extra space for the array. Where N is the length of the string.

Method 2 (Dynamic Programming):
Though we have only 100-digit numbers, for longer examples larger than that, our program might exceed the given time limit. 
Thus, we optimize our code by using a dynamic programming approach.
Let 

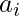
Be the ith digit of the sample. We generate a matrix dp[i][j], 1<=i<=n and 0<=j<8. The value of dp is true if we can cross out some digits from the prefix of length i such that the remaining number gives j modulo eight, and false otherwise. For a broad understanding of the concept, if at an index, we find element modulo 8 for that index we put the value of 

For all other numbers, we build on a simple concept that either addition of that digit will contribute information of a number divisible by 8, or it shall be left out.

Note: We also have to keep it in mind that we cannot change the order
Now,  

if we add the current digit to the previous result.

if we exclude the current digit in our formation.
Now, if such a number shall exist, we will get a “true” for any i in dp[i][0]

C++

// C++ program to find if there is a subsequence
// of digits divisible by 8.
#include <bits/stdc++.h>
using namespace std;

// Function takes in an array of numbers,
// dynamically goes on the location and
// makes combination of numbers.
bool isSubSeqDivisible(string str)
{
    int n = str.length();
    int dp[n + 1][10];
    memset(dp, 0, sizeof(dp));

    // Converting string to integer array for ease
    // of computations (Indexing in arr[] is
    // considered to be starting from 1)
    int arr[n + 1];
    for (int i = 1; i <= n; i++)
        arr[i] = str[i - 1] - '0';

    for (int i = 1; i <= n; i++) {

        dp[i][arr[i] % 8] = 1;
        for (int j = 0; j < 8; j++) {

            // If we consider the number in our combination,
            // we add it to the previous combination
            if (dp[i - 1][j] > dp[i][(j * 10 + arr[i]) % 8])
                dp[i][(j * 10 + arr[i]) % 8] = dp[i - 1][j];

            // If we exclude the number from our combination
            if (dp[i - 1][j] > dp[i][j])
                dp[i][j] = dp[i - 1][j];
        }
    }

    for (int i = 1; i <= n; i++) {

        // If at dp[i][0], we find value 1/true, it shows
        // that the number exists at the value of 'i'
        if (dp[i][0] == 1)
            return true;
    }

    return false;
}

// Driver function
int main()
{
    string str = "3144";
    if (isSubSeqDivisible(str))
        cout << "Yes";
    else
        cout << "No";
    return 0;
}

Java

// Java program to find if there is a
// subsequence of digits divisible by 8.
import java.io.*;
import java.util.*;

class GFG {

    // Function takes in an array of numbers,
    // dynamically goes on the location and
    // makes combination of numbers.
    static boolean isSubSeqDivisible(String str)
    {

        int n = str.length();
        int dp[][] = new int[n + 1][10];

        // Converting string to integer array
        // for ease of computations (Indexing in
        // arr[] is considered to be starting
        // from 1)
        int arr[] = new int[n + 1];
        for (int i = 1; i <= n; i++)
            arr[i] = (int)(str.charAt(i - 1) - '0');

        for (int i = 1; i <= n; i++) {

            dp[i][arr[i] % 8] = 1;
            for (int j = 0; j < 8; j++) {

                // If we consider the number in
                // our combination, we add it to
                // the previous combination
                if (dp[i - 1][j] > dp[i][(j * 10
                                          + arr[i])
                                         % 8])
                    dp[i][(j * 10 + arr[i]) % 8]
                        = dp[i - 1][j];

                // If we exclude the number from
                // our combination
                if (dp[i - 1][j] > dp[i][j])
                    dp[i][j] = dp[i - 1][j];
            }
        }

        for (int i = 1; i <= n; i++) {

            // If at dp[i][0], we find value 1/true,
            // it shows that the number exists at
            // the value of 'i'
            if (dp[i][0] == 1)
                return true;
        }

        return false;
    }

    // Driver function
    public static void main(String args[])
    {
        String str = "3144";
        if (isSubSeqDivisible(str))
            System.out.println("Yes");
        else
            System.out.println("No");
    }
}

/* This code is contributed by Nikita Tiwari.*/

Python3

# Python3 program to find
# if there is a subsequence
# of digits divisible by 8.

# Function takes in an array of numbers,
# dynamically goes on the location and
# makes combination of numbers.
def isSubSeqDivisible(str):
    n = len(str)
    dp = [[0 for i in range(10)]
             for i in range(n + 1)]

    # Converting string to integer
    # array for ease of computations
    # (Indexing in arr[] is considered
    # to be starting from 1)
    arr = [0 for i in range(n + 1)]
    for i in range(1, n + 1):
        arr[i] = int(str[i - 1]);

    for i in range(1, n + 1):
        dp[i][arr[i] % 8] = 1;
        for j in range(8):

            # If we consider the number
            # in our combination, we add
            # it to the previous combination
            if (dp[i - 1][j] > dp[i][(j * 10 + arr[i]) % 8]):
                dp[i][(j * 10 + arr[i]) % 8] = dp[i - 1][j]

            # If we exclude the number
            # from our combination
            if (dp[i - 1][j] > dp[i][j]):
                dp[i][j] = dp[i - 1][j]

    for i in range(1, n + 1):

        # If at dp[i][0], we find
        # value 1/true, it shows
        # that the number exists
        # at the value of 'i'
        if (dp[i][0] == 1):
            return True
    return False

# Driver Code
str = "3144"
if (isSubSeqDivisible(str)):
    print("Yes")
else:
    print("No")

# This code is contributed
# by sahilshelangia

C#

// C# program to find if there is a
// subsequence of digits divisible by 8.
using System;

class GFG {

    // Function takes in an array of numbers,
    // dynamically goes on the location and
    // makes combination of numbers.
    static bool isSubSeqDivisible(String str)
    {

        int n = str.Length;
        int[, ] dp = new int[n + 1, 10];

        // Converting string to integer array
        // for ease of computations (Indexing in
        // arr[] is considered to be starting
        // from 1)
        int[] arr = new int[n + 1];
        for (int i = 1; i <= n; i++)
            arr[i] = (int)(str[i - 1] - '0');

        for (int i = 1; i <= n; i++) {
            dp[i, arr[i] % 8] = 1;
            for (int j = 0; j < 8; j++) {

                // If we consider the number in
                // our combination, we add it to
                // the previous combination
                if (dp[i - 1, j] > dp[i, (j * 10
                                          + arr[i])
                                             % 8])
                    dp[i, (j * 10 + arr[i]) % 8]
                        = dp[i - 1, j];

                // If we exclude the number from
                // our combination
                if (dp[i - 1, j] > dp[i, j])
                    dp[i, j] = dp[i - 1, j];
            }
        }

        for (int i = 1; i <= n; i++) {

            // If at dp[i][0], we find value
            // 1/true, it shows that the number
            // exists at the value of 'i'
            if (dp[i, 0] == 1)
                return true;
        }

        return false;
    }

    // Driver function
    public static void Main()
    {
        string str = "3144";

        if (isSubSeqDivisible(str))
            Console.WriteLine("Yes");
        else
            Console.WriteLine("No");
    }
}

// This code is contributed by vt_m.

PHP

<?php
// PHP program to find if there
// is a subsequence of digits
// divisible by 8.

// Function takes in an array of numbers,
// dynamically goes on the location and
// makes combination of numbers.
function isSubSeqDivisible($str)
{
    $n = strlen($str);
    $dp = array_fill(0, $n + 1,
          array_fill(0, 10, NULL));

    // Converting string to integer
    // array for ease of computations
    // (Indexing in arr[] is considered
    // to be starting from 1)
    $arr = array_fill(0, ($n + 1), NULL);
    for ($i = 1; $i <= $n; $i++)
        $arr[$i] = $str[$i - 1] - '0';

    for ($i = 1; $i <= $n; $i++)
    {
        $dp[$i][$arr[$i] % 8] = 1;
        for ($j = 0; $j < 8; $j++)
        {

            // If we consider the number in
            // our combination, we add it to
            // the previous combination
            if ($dp[$i - 1][$j] > $dp[$i][($j * 10 +
                                           $arr[$i]) % 8])
                $dp[$i][($j * 10 +
                         $arr[$i]) % 8] = $dp[$i - 1][$j];

            // If we exclude the number
            // from our combination
            if ($dp[$i - 1][$j] > $dp[$i][$j])
                $dp[$i][$j] = $dp[$i - 1][$j];
        }
    }

    for ($i = 1; $i <= $n; $i++)
    {

        // If at dp[i][0], we find value 1/true,
        // it shows that the number exists at
        // the value of 'i'
        if ($dp[$i][0] == 1)
            return true;
    }

    return false;
}

// Driver Code
$str = "3144";
if (isSubSeqDivisible($str))
    echo "Yes";
else
    echo "No";

// This code is contributed
// by ChitraNayal
?>

Javascript

<script>
    // Javascript program to find if there is a
    // subsequence of digits divisible by 8.

    // Function takes in an array of numbers,
    // dynamically goes on the location and
    // makes combination of numbers.
    function isSubSeqDivisible(str)
    {

        let n = str.length;
        let dp = new Array(n + 1);
        for(let i = 0; i < 10; i++)
        {
            dp[i] = new Array(10);
            for(let j = 0; j < 10; j++)
            {
                dp[i][j] = 0;
            }
        }

        // Converting string to integer array
        // for ease of computations (Indexing in
        // arr[] is considered to be starting
        // from 1)
        let arr = new Array(n + 1);
        for (let i = 1; i <= n; i++)
            arr[i] = (str[i - 1].charCodeAt() - '0'.charCodeAt());

        for (let i = 1; i <= n; i++) {

            dp[i][arr[i] % 8] = 1;
            for (let j = 0; j < 8; j++) {

                // If we consider the number in
                // our combination, we add it to
                // the previous combination
                if (dp[i - 1][j] > dp[i][(j * 10 + arr[i]) % 8])
                    dp[i][(j * 10 + arr[i]) % 8] = dp[i - 1][j];

                // If we exclude the number from
                // our combination
                if (dp[i - 1][j] > dp[i][j])
                    dp[i][j] = dp[i - 1][j];
            }
        }

        for (let i = 1; i <= n; i++) {

            // If at dp[i][0], we find value 1/true,
            // it shows that the number exists at
            // the value of 'i'
            if (dp[i][0] == 1)
                return true;
        }

        return false;
    }

    let str = "3144";
    if (isSubSeqDivisible(str))
      document.write("Yes");
    else
      document.write("No");

</script>

Output

Yes

Time Complexity: O(n), as using the dynamic approach, our time complexity cuts down to O(8*n) as we are using linear traversal. Where 8 is from which the number should be divisible and n is the length of our input.

Auxiliary Space: O(n), as we are using extra space for the dp matrix. Where N is the length of our input.

Method 3
For this problem, we simply need to check if there exists a two-digit subsequence divisible by 8 (divisibility test for 8) 
We first find all the 2 digit numbers divisible by 8 and map the tens place digit with unit place digit 
i.e :- 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96 
Ignore 48 as 8 is always divisible by 8 similarly 80 and 88 have 8 in them which make such subsequence always divisible by 8 
So we map 1 to 6, 2 to 4, 3 to 2, and so on using map i.e stl map in C++. 
After building the map we traverse the string from the last index and check if the mapped value of the present index number is visited or not hence we need a visited array for this which will store true if the number is visited, else false 
eg:- 3769 
first char from the last index is 9 so we check if 6 is visited (i.e 96 is subsequence or not), we mark 9 in visited array 
next char is 6 so we check is 4 visited (i.e 64), we mark 6 in the visited array 
next char is 7 so we check is 2 visited (i.e 72), we mark 7 in the visited array 
next char is 3 so we check is 6 visited (i.e 36), yes 6 is marked hence we print Yes.

C++

// C++ program to check if given string
// has a subsequence divisible by 8
#include<bits/stdc++.h>
using namespace std;
// Driver function
int main(){

    string str = "129365";

    // map key will be tens place digit of number
        // that is divisible by 8 and value will
        // be units place digit
    map<int, int> mp;

    // For filling the map let start
        // with initial value 8
    int no = 8;

    while(no < 100){
        no = no + 8;

        // key is digit at tens place and value is
            // digit at units place mp.insert({key, value})
        mp.insert({(no / 10) % 10, no % 10});
    }

    // Create a hash to check if we visited a number
    vector<bool> visited(10, false);

    int i;
    // Iterate from last index to 0th index
    for(i = str.length() - 1; i >= 0; i--){

        // If 8 is present in string then
            // 8 divided 8 hence print yes
        if(str[i] == '8')
           {
               cout << "Yes";
                break;
           }

        // considering present character as the second
        // digit of two digits no we check if the value
        // of this key is marked in hash or not
        // If marked then we a have a number divisible by 8
        if(visited[mp[str[i] - '0']]){
            cout << "Yes";
            break;
        }
        visited[str[i] - '0'] = true;

    }
    // If no subsequence divisible by 8
    if(i == -1)
        cout << "No";
    return 0;
}

Java

// Java program to check if
// given String has a subsequence
// divisible by 8
import java.util.*;
class GFG{

// Driver code
public static void main(String[] args)
{
  String str = "129365";

  // map key will be tens place
  // digit of number that is
  // divisible by 8 and value will
  // be units place digit
  HashMap<Integer,
          Integer> mp = new HashMap<Integer,
                                    Integer>();

  // For filling the map let start
  // with initial value 8
  int no = 8;

  while(no < 100)
  {
    no = no + 8;

    // key is digit at tens place
    // and value is digit at units
    // place mp.add({key, value})
    //if(mp.containsKey((no / 10) % 10))
    mp.put((no / 10) % 10, no % 10);
  }

  // Create a hash to check if
  // we visited a number
  boolean[] visited = new boolean[10];

  int i;

  // Iterate from last index
  // to 0th index
  for(i = str.length() - 1;
      i >= 0; i--)
  {
    // If 8 is present in String then
    // 8 divided 8 hence print yes
    if(str.charAt(i) == '8')
    {
      System.out.print("Yes");
      break;
    }

    // considering present character
    // as the second digit of two
    // digits no we check if the value
    // of this key is marked in hash or not
    // If marked then we a have a number
    // divisible by 8
    if(visited[mp.get(str.charAt(i)- '0')])
    {
      System.out.print("Yes");
      break;
    }
    visited[str.charAt(i) - '0'] = true;

  }
  // If no subsequence divisible
  // by 8
  if(i == -1)
    System.out.print("No");
}
}

// This code is contributed by shikhasingrajput

Python3

# Python3 program to check if given string
# has a subsequence divisible by 8
Str = "129365"

# map key will be tens place digit of number
# that is divisible by 8 and value will
# be units place digit
mp = {}

# For filling the map let start
# with initial value 8
no = 8

while(no < 100) :
    no = no + 8

    # key is digit at tens place and value is
    # digit at units place mp.insert({key, value})
    mp[(no // 10) % 10] = no % 10

# Create a hash to check if we visited a number
visited = [False] * 10

# Iterate from last index to 0th index
for i in range(len(Str) - 1, -1, -1) :

    # If 8 is present in string then
    # 8 divided 8 hence print yes
    if(Str[i] == '8') :

        print("Yes", end = "")
        break

    # considering present character as the second
    # digit of two digits no we check if the value
    # of this key is marked in hash or not
    # If marked then we a have a number divisible by 8
    if visited[mp[ord(Str[i]) - ord('0')]] :
        print("Yes", end = "")
        break

    visited[ord(Str[i]) - ord('0')] = True

# If no subsequence divisible by 8
if(i == -1) :
    print("No")

    # This code is contributed by divyeshrabadiya07

C#

// C# program to check if given
// String has a subsequence
// divisible by 8
using System;
using System.Collections.Generic;

class GFG{

// Driver code
public static void Main(String[] args)
{
    String str = "129365";

    // Map key will be tens place
    // digit of number that is
    // divisible by 8 and value will
    // be units place digit
    Dictionary<int,
               int> mp = new Dictionary<int,
                                        int>();

    // For filling the map let start
    // with initial value 8
    int no = 8;

    while (no < 100)
    {
        no = no + 8;

        // Key is digit at tens place
        // and value is digit at units
        // place mp.Add({key, value})
        if (mp.ContainsKey((no / 10) % 10))
            mp[(no / 10) % 10] = no % 10;
        else
            mp.Add((no / 10) % 10, no % 10);
    }

    // Create a hash to check if
    // we visited a number
    bool[] visited = new bool[10];

    int i;

    // Iterate from last index
    // to 0th index
    for(i = str.Length - 1; i >= 0; i--)
    {

        // If 8 is present in String then
        // 8 divided 8 hence print yes
        if (str[i] == '8')
        {
            Console.Write("Yes");
            break;
        }

        // Considering present character
        // as the second digit of two
        // digits no we check if the value
        // of this key is marked in hash or not
        // If marked then we a have a number
        // divisible by 8
        if (visited[mp[str[i] - '0']])
        {
            Console.Write("Yes");
            break;
        }
        visited[str[i] - '0'] = true;
    }

    // If no subsequence divisible
    // by 8
    if (i == -1)
        Console.Write("No");
}
}

// This code is contributed by Princi Singh

Javascript

<script>

// Javascript program to check if
// given String has a subsequence
// divisible by 8


    // Driver code
    let str = "129365";

    // map key will be tens place
  // digit of number that is
  // divisible by 8 and value will
  // be units place digit
  let mp = new Map();

  // For filling the map let start
  // with initial value 8
  let no = 8;

  while(no < 100)
  {
    no = no + 8;

    // key is digit at tens place
    // and value is digit at units
    // place mp.add({key, value})
    //if(mp.containsKey((no / 10) % 10))
    mp.set((Math.floor(no / 10)) % 10, no % 10);
  }

  // Create a hash to check if
  // we visited a number
  let visited = new Array(10);
  for(let i=0;i<visited.length;i++)
  {
      visited[i]=false;
  }

  let i;

  // Iterate from last index
  // to 0th index
  for(i = str.length - 1;
      i >= 0; i--)
  {
    // If 8 is present in String then
    // 8 divided 8 hence print yes
    if(str[i] == '8')
    {
      document.write("Yes");
      break;
    }

    // considering present character
    // as the second digit of two
    // digits no we check if the value
    // of this key is marked in hash or not
    // If marked then we a have a number
    // divisible by 8
    if(visited[mp.get(str[i].charCodeAt(0)-
    '0'.charCodeAt(0))])
    {
      document.write("Yes");
      break;
    }
    visited[str[i].charCodeAt(0) -
    '0'.charCodeAt(0)] = true;

  }
  // If no subsequence divisible
  // by 8
  if(i == -1)
    document.write("No");

    // This code is contributed by rag2127

</script>

Output

Yes

Time Complexity: O(n), as we are using a loop to traverse n times. Where n is the length of our input.

Auxiliary Space: O(1), as if you take a close look, the visited array will always have 10 fields and the map will always have the same size, hence space complexity will O(1).