Gate IT 2008

Question 1

A set of Boolean connectives is functionally complete if all Boolean functions can be synthesized using those. Which of the following sets of connectives is NOT functionally complete?

• EX-NOR
• implication, negation
• OR, negation
• NAND

Question 2

A sample space has two events A and B such that probabilities P(A ∩ B) = 1/2, P(A\') = 1/3, P(B\') = 1/3. What is P(A U B)?

• 11/12
• 10/12
• 9/12
• 8/12

Question 3

What is the chromatic number of the following graph?

• 2
• 3
• 4
• 5

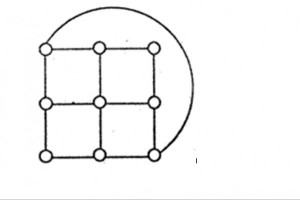
Question 4

What is the size of the smallest MIS(Maximal Independent Set) of a chain of nine nodes?

• 5
• 4
• 3
• 2

Question 5

Which of the following regular expressions describes the language over {0, 1} consisting of strings that contain exactly two 1\'s?

• (0 + 1) * 11(0 + 1) *
• 0 * 110 *
• 0 * 10 * 10 *
• (0 + 1) * 1(0 + 1) * 1 (0 + 1) *

Question 6

Let N be an NFA with n states and let M be the minimized DFA with m states recognizing the same language. Which of the following in NECESSARILY true?

• m ≤ 2ⁿ
• n ≤ m
• M has one accept state
• m = 2ⁿ

Question 7

The following bit pattern represents a floating point number in IEEE 754 single precision format 1 10000011 101000000000000000000000 The value of the number in decimal form is

• -10
• -13
• -26
• None of these

Question 8

Consider the following Boolean function of four variables f(A, B, C, D) = Σ(2, 3, 6, 7, 8, 9, 10, 11, 12, 13) The function is

• independent of one variable
• independent of two variables
• independent of three variable
• dependent on all the variables

Question 9

What Boolean function does the circuit below realize ?

• xz+x\'z\'
• xz\'+x\'z
• x\'y\'+yz
• xy+y\'z\'

Question 10

Arrange the following functions in increasing asymptotic order:
A. n^1/3
B. eⁿ
C. n^7/4
D. n log⁹n
E. 1.0000001ⁿ

• A, D, C, E, B
• D, A, C, E, B
• A, C, D, E, B
• A, C, D, B, E