GATE-CS-2005

  • Last Updated : 27 Jul, 2021

123456789
Question 1
What does the following C-statement declare? [1 mark]
int ( * f) (int * ) ;

A
A function that takes an integer pointer as argument and returns an integer.
B
A function that takes an integer as argument and returns an integer pointer.
C
A pointer to a function that takes an integer pointer as argument and returns an integer.
D
A function that takes an integer pointer as argument and returns a function pointer
C Pointer Basics    GATE-CS-2005    
Discuss it


Question 1 Explanation: 
The steps to read complicated declarations :
1)Convert C declaration to postfix format and read from left to right.
2)To convert expression to postfix, start from innermost parenthesis, If innermost parenthesis is not present then start from declarations name and go right first. When first ending parenthesis encounters then go left. Once the whole parenthesis is parsed then come out from parenthesis.
3)Continue until complete declaration has been parsed.
At First, we convert the following given declaration into postfix:
int ( * f) (int * )
Since there is no innermost bracket, so first we take declaration name f, so print “f” and then go to the right, since there is nothing to parse, so go to the left. There is * at the left side, so print “*”.Come out of parenthesis. Hence postfix notation of given declaration can be written as follows:
f * (int * ) int
Meaning: f is a pointer to function (which takes one argument of int pointer type) returning int .
Refer http://www.geeksforgeeks.org/complicated-declarations-in-c/
This solution is contributed by Nirmal Bharadwaj.
Question 2
An Abstract Data Type (ADT) is:
A
Same as an abstract class
B
A data type that cannot be instantiated
C
A data type type for which only the operations defined on it can be used, but none else
D
All of the above
Data Structures Misc    GATE-CS-2005    
Discuss it


Question 3
A common property of logic programming languages and functional languages is:
A
both are procedural languages
B
both are based on λ-calculus
C
both are declarative
D
both use Horn-clauses
Principles of Programming Languages    GATE-CS-2005    
Discuss it


Question 4
Which one of the following are essential features of an object-oriented programming language? (GATE CS 2005)
(i) Abstraction and encapsulation
(ii) Strictly-typedness
(iii) Type-safe property coupled with sub-type rule
(iv) Polymorphism in the presence of inheritance
Answer (b)
Abstraction, Encapsulation, Polymorphism and Inheritance are the essential features of a OOP Language (See the Wiki page for OOP).
A
(i) and (ii) only
B
(i) and (iv) only
C
(i), (ii) and (iv) only
D
(i), (iii) and (iv) only
GATE-CS-2005    OOP Concepts    
Discuss it


Question 4 Explanation: 
Abstraction, Encapsulation, Polymorphism and Inheritance are the essential features of a OOP Language (See the Wiki page for OOP).
Question 5
A program P reads in 500 integers in the range [0..100] representing the scores of 500 students. It then prints the frequency of each score above 50. What would be the best way for P to store the frequencies?
A
An array of 50 numbers
B
An array of 100 numbers
C
An array of 500 numbers
D
A dynamically allocated array of 550 numbers
GATE-CS-2005    
Discuss it


Question 6
An undirected graph C has n nodes. Its adjacency matrix is given by an n × n square matrix whose
(i) diagonal elements are 0's, and
(ii) non-diagonal elements are l's.
Which one of the following is TRUE?
A
Graph G has no minimum spanning tree (MST)
B
Graph G has a unique MST of cost n-1
C
Graph G has multiple distinct MSTs, each of cost n-1
D
Graph G has multiple spanning trees of different costs
GATE-CS-2005    
Discuss it


Question 7
The time complexity of computing the transitive closure of a binary relation on a set of n elements is known to be
A
O (n)
B
O (n log n)
C
O(n3/2)
D
O(n3)
GATE-CS-2005    
Discuss it


Question 8
Let A, B and C be non-empty sets and let X = (A - B) - C and Y = (A - C) - (B - C).
Which one of the following is TRUE?
A
X = Y
B
X ⊂ Y
C
Y ⊂ X
D
none of these
Set Theory & Algebra    GATE-CS-2005    
Discuss it


Question 8 Explanation: 
We can solve it by making Venn diagram
Question 9
The following is the Hasse diagram of the poset [{a, b, c, d, e}, ≤]
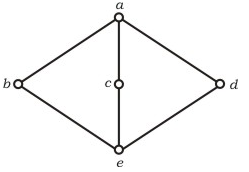
GATECS2005Q9
The poset is
A
not a lattice
B
a lattice but not a distributive lattice
C
a distributive lattice but not a Boolean algebra
D
a Boolean algebra
Set Theory & Algebra    GATE-CS-2005    
Discuss it


Question 9 Explanation: 
It is a lattice but not a distributive lattice.

Table for Join Operation of above Hesse diagram

V |a b c d e
________________
a |a a a a a
b |a b a a b
c |a a c a c
d |a a a d d
e |a b c d e

Table for Meet Operation of above Hesse diagram

^ |a b c d e
_______________
a |a b c d e
b |b b e e e
c |c e c e e
d |d e e d e
e |e e e e e

Therefore for any two element p, q in the lattice (A,<=)

p <= p V q ; p^q <= p

This satisfies for all element (a,b,c,d,e).

which has 'a' as unique least upper bound and 'e' as unique 
greatest lower bound.

The given lattice doesn't obey distributive law, so it is 
not distributive lattice,

Note that for b,c,d we have distributive law

b^(cVd) = (b^c) V (b^d). From the diagram / tables given above 
we can verify as follows,

(i) L.H.S. = b ^ (c V d) = b ^ a = b

(ii) R.H.S. = (b^c) V (b^d) = e v e = e

b != e which contradict the distributive law. 
Hence it is not distributive lattice.

so, option (B) is correct. 
Question 10
Let G be a simple connected planar graph with 13 vertices and 19 edges. Then, the number of faces in the planar embedding of the graph is
A
6
B
8
C
9
D
13
Graph Theory    GATE-CS-2005    
Discuss it


Question 10 Explanation: 
An undirected graph is called a planar graph if it can be drawn on a paper without having two edges cross and such a drawing is called Planar Embedding. We say that a graph can be embedded in the plane, if it planar. A planar graph divides the plane into regions (bounded by the edges), called faces. Graph K4 is palanar graph, because it has a planar embedding as shown in
figure below.
P_graph
Euler's Formula : For any polyhedron that doesn't intersect itself (Connected Planar Graph),the
• Number of Faces(F)
• plus the Number of Vertices (corner points) (V)
• minus the Number of Edges(E)
, always equals 2. This can be written: F + V − E = 2.
Solution :
Here as given, F=?,V=13 and E=19
-> F+13-19=2
-> F=8
So Answer is (B).
This solution is contributed by Nirmal Bharadwaj
We can apply Euler's Formula of planar graphs. The formula is v − e + f = 2.
There are 90 questions to complete.
123456789
My Personal Notes
arrow_drop_up


Writing code in comment? Please use ide.geeksforgeeks.org, generate link and share the link here.