Given two strings X and Y. The task is to find the length of the longest subsequence of string X which is a substring in sequence Y.
Examples:
Input : X = "ABCD", Y = "BACDBDCD"
Output : 3
"ACD" is longest subsequence of X which
is substring of Y.
Input : X = "A", Y = "A"
Output : 1
PREREQUISITES: Longest common subsequence problem will help you understand this problem in a snap 🙂
Method 1 (Brute Force):
Use brute force to find all the subsequences of X and for each subsequence check whether it is a substring of Y or not. If it is a substring of Y, maintain a maximum length variable and compare its length.
Time Complexity: O(2^n *(n*m))
Method 2: (Recursion):
Let n be the length of X and m be the length of Y. We will make a recursive function as follows with 4 arguments and the return type is int as we will get the length of a maximum possible subsequence of X which is the Substring of Y. We will take judgment for further process based on the last char in strings by using n-1 and m-1.
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
....
return ans;
}
For recursion we need 2 things, we will make 1st the base case and 2nd is calls on smaller input (for that we will see the choice diagram).
BASE CASE:
By seeing the argument of function we can see only 2 arguments that will change while recursion calls, i.e. lengths of both strings. So for the base case think of the smallest input we can give. You’ll see the smallest input is 0, i.e. empty lengths. hence when n == 0 or m == 0 is the base case. n and m can’t be less than zero. Now we know the condition and we need to return the length of subsequence as per the question. if the length is 0, then means one of the string is empty, and there is no common subsequence possible, so we have to return 0 for the same.
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
if (n==0 || m==0) return 0;
....
return ans;
}
CHILDREN CALLS:
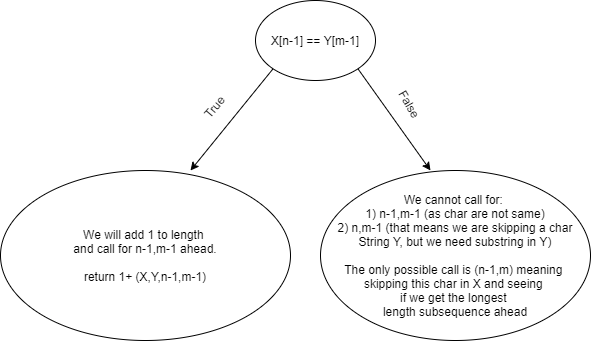
Choice Diagram
We can see how to make calls by seeing if the last char of both strings are the same or not. We can see how this is slightly different from the LCS (Longest Common Subsequence) question.
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
// Base Case
if (n==0 || m==0) return 0;
// Calls on smaller inputs
// if the last char of both strings are equal
if(X[n-1] == Y[m-1])
{
return 1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
}
// if the last char of both strings are not equal
else
{
return maxSubsequenceSubstring(X,Y,n-1,m);
}
}
Now here is the main crux of the question, we can see we are calling for X[0..n] and Y[0..m], in our recursion function it will return the answer of maximum length of the subsequence of X, and Substring of Y (and the ending char of that substring of Y ends at length m). This is very important as we want to find all intermediary substrings also. hence we need to use a for loop where we will call the above function for all the lengths from 0 to m of Y, and return the maximum of the answer there. Here is the final code in C++ for the same.
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
int maxSubsequenceSubstring(string &X,string &Y,int n,int m)
{
if (n==0 || m==0) return 0;
if(X[n-1] == Y[m-1])
{
return 1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
}
else
{
return maxSubsequenceSubstring(X,Y,n-1,m);
}
}
int main()
{
string X = "abcd";
string Y = "bacdbdcd";
int n = X.size(),m = Y.size();
int maximum_length = 0;
for(int i = 0;i<=m;i++)
{
int temp_ans = maxSubsequenceSubstring(X,Y,n,i);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
cout<<"Length for maximum possible Subsequence of string X which is Substring of Y -> "<<maximum_length;
return 0;
}
|
Java
import java.util.*;
class GFG {
static int maxSubsequenceSubString(String X, String Y,
int n, int m)
{
if (n == 0 || m == 0)
return 0;
if (X.charAt(n - 1) == Y.charAt(m - 1)) {
return 1
+ maxSubsequenceSubString(X, Y, n - 1,
m - 1);
}
else {
return maxSubsequenceSubString(X, Y, n - 1, m);
}
}
public static void main(String[] args)
{
String X = "abcd";
String Y = "bacdbdcd";
int n = X.length(), m = Y.length();
int maximum_length
= 0;
for (int i = 0; i <= m;
i++)
{
int temp_ans
= maxSubsequenceSubString(X, Y, n, i);
if (temp_ans > maximum_length)
maximum_length = temp_ans;
}
System.out.print(
"Length for maximum possible Subsequence of String X which is SubString of Y->"
+ maximum_length);
}
}
|
Python3
def maxSubsequenceSubstring(X, Y, n, m):
if (n == 0 or m == 0):
return 0
if(X[n - 1] == Y[m - 1]):
return 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1)
else:
return maxSubsequenceSubstring(X, Y, n - 1, m)
X = "abcd"
Y = "bacdbdcd"
n, m = len(X), len(Y)
maximum_length = 0
for i in range(m + 1):
temp_ans = maxSubsequenceSubstring(X, Y, n, i)
if(temp_ans > maximum_length):
maximum_length = temp_ans
print(f"Length for maximum possible Subsequence of string X which is Substring of Y -> {maximum_length}")
|
C#
using System;
public class GFG {
static int maxSubsequenceSubString(String X, String Y,
int n, int m)
{
if (n == 0 || m == 0)
return 0;
if (X[n - 1] == Y[m - 1]) {
return 1
+ maxSubsequenceSubString(X, Y, n - 1,
m - 1);
}
else {
return maxSubsequenceSubString(X, Y, n - 1, m);
}
}
public static void Main(String[] args)
{
String X = "abcd";
String Y = "bacdbdcd";
int n = X.Length, m = Y.Length;
int maximum_length
= 0;
for (int i = 0; i <= m;
i++)
{
int temp_ans
= maxSubsequenceSubString(X, Y, n, i);
if (temp_ans > maximum_length)
maximum_length = temp_ans;
}
Console.Write(
"Length for maximum possible Subsequence of String X which is SubString of Y->"
+ maximum_length);
}
}
|
Javascript
<script>
function maxSubsequenceSubstring(X,Y,n,m)
{
if (n==0 || m==0) return 0;
if(X[n-1] == Y[m-1])
{
return 1 + maxSubsequenceSubstring(X,Y,n-1,m-1);
}
else
{
return maxSubsequenceSubstring(X,Y,n-1,m);
}
}
let X = "abcd";
let Y = "bacdbdcd";
let n = X.length,m = Y.length;
let maximum_length = 0;
for(let i = 0;i<=m;i++)
{
let temp_ans = maxSubsequenceSubstring(X,Y,n,i);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
document.write("Length for maximum possible Subsequence of string X which is Substring of Y -> "+ maximum_length);
</script>
|
OutputLength for maximum possible Subsequence of string X which is Substring of Y -> 3
Time Complexity: O(n*m) (For every call in the recursion function we are decreasing n, hence we will reach the base case exactly after n calls, and we are using for loop for m times for the different lengths of string Y).
Space Complexity: O(n) (For recursion calls we are using stacks for each call).
Method 3: (Dynamic Programming):
Submethod 1:- Memoization
NOTE: Must see the above recursion solution to understand its optimization as Memoization
From the above recursion solution, there are multiple calls and further, we are using recursion in for loop, there is a high probability we have already solved the answer for a call. hence to optimize our recursion solution we will use? (See we have only 2 arguments that vary throughout the calls, hence the dimension of the array is 2 and the size is 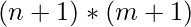 because we need to store answers for all possible calls from 0..n and 0..m). Hence it is a 2D array.
because we need to store answers for all possible calls from 0..n and 0..m). Hence it is a 2D array.
we can use vectors for the same or dynamic allocation of the array.
// initialise a vector like this
vector<vector<int>> dp(n+1,vector<int>(m+1,-1));
// or Dynamic allocation
int **dp = new int*[n+1];
for(int i = 0;i<=n;i++)
{
dp[i] = new int[m+1];
for(int j = 0;j<=m;j++)
{
dp[i][j] = -1;
}
}
By initializing the 2D vector we will use this array as the 5th argument in recursion and store our answer. also, we have filled it with -1, which means we have not solved this call hence use traditional recursion for it, if dp[n][m] at any call is not -1, means we have already solved the call, hence use the answer of dp[n][m].
// In recursion calls we will check for if we have solved the answer for the call or not
if(dp[n][m] != -1) return dp[n][m];
// Else we will store the result and return that back from this call
if(X[n-1] == Y[m-1])
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
else
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
Code for memoization is here:
C++
#include<bits/stdc++.h>
using namespace std;
int maxSubsequenceSubstring(string &X,string &Y,int n,int m,vector<vector<int>>& dp)
{
if (n==0 || m==0) return 0;
if(dp[n][m] != -1) return dp[n][m];
if(X[n-1] == Y[m-1])
{
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
}
else
{
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
}
}
int main()
{
string X = "abcd";
string Y = "bacdbdcd";
int n = X.size(),m = Y.size();
int maximum_length = 0;
vector<vector<int>> dp(n+1,vector<int>(m+1,-1));
for(int i = 0;i<=m;i++)
{
int temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
cout<<"Length for maximum possible Subsequence of string X which is Substring of Y -> "<<maximum_length;
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static int maxSubsequenceSubstring(String X,String Y,int n,int m,int dp[][])
{
if (n==0 || m==0) return 0;
if(dp[n][m] != -1) return dp[n][m];
if(X.charAt(n-1) == Y.charAt(m-1))
{
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
}
else
{
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
}
}
public static void main(String args[])
{
String X = "abcd";
String Y = "bacdbdcd";
int n = X.length(),m = Y.length();
int maximum_length = 0;
int dp[][] = new int[n+1][m+1];
for(int i = 0; i < n + 1; i++){
Arrays.fill(dp[i], -1);
}
for(int i = 0;i<=m;i++)
{
int temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
System.out.println("Length for maximum possible Subsequence of string X which is Substring of Y -> "+maximum_length);
}
}
|
Python3
def maxSubsequenceSubstring(X, Y, n, m, dp):
if (n == 0 or m == 0):
return 0
if(dp[n][m] != -1):
return dp[n][m]
if(X[n - 1] == Y[m - 1]):
dp[n][m] = 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1, dp)
return dp[n][m]
else:
dp[n][m] = maxSubsequenceSubstring(X, Y, n - 1, m, dp)
return dp[n][m]
X = "abcd"
Y = "bacdbdcd"
n,m = len(X),len(Y)
maximum_length = 0
dp = [[-1 for i in range(m+1)]for j in range(n+1)]
for i in range(m+1):
temp_ans = maxSubsequenceSubstring(X, Y, n, i, dp)
if(temp_ans > maximum_length):
maximum_length = temp_ans
print("Length for maximum possible Subsequence of string X which is Substring of Y -> "+str(maximum_length))
|
C#
using System;
class GFG
{
static int maxSubsequenceSubstring(string X, string Y, int n, int m, int[,] dp)
{
if (n == 0 || m == 0) return 0;
if (dp[n, m] != -1) return dp[n, m];
if (X[n - 1] == Y[m - 1])
{
return dp[n, m] = 1 + maxSubsequenceSubstring(X, Y, n - 1, m - 1, dp);
}
else
{
return dp[n, m] = maxSubsequenceSubstring(X, Y, n - 1, m, dp);
}
}
public static void Main(string[] args)
{
string X = "abcd";
string Y = "bacdbdcd";
int n = X.Length, m = Y.Length;
int maximum_length = 0;
int[,] dp = new int[n + 1, m + 1];
for (int i = 0; i < n + 1; i++)
{
for (int j = 0; j < m + 1; j++)
{
dp[i, j] = -1;
}
}
for (int i = 0; i <= m; i++)
{
int temp_ans = maxSubsequenceSubstring(X, Y, n, i, dp);
if (temp_ans > maximum_length) maximum_length = temp_ans;
}
Console.WriteLine("Length for maximum possible Subsequence of string X which is Substring of Y -> " + maximum_length);
}
}
|
Javascript
<script>
function maxSubsequenceSubstring(X,Y,n,m,dp)
{
if (n==0 || m==0) return 0;
if(dp[n][m] != -1) return dp[n][m];
if(X[n-1] == Y[m-1])
{
return dp[n][m] = 1 + maxSubsequenceSubstring(X,Y,n-1,m-1,dp);
}
else
{
return dp[n][m] = maxSubsequenceSubstring(X,Y,n-1,m,dp);
}
}
let X = "abcd";
let Y = "bacdbdcd";
let n = X.length,m = Y.length;
let maximum_length = 0;
let dp = new Array(n+1);
for(let i=0;i<n+1;i++){
dp[i] = new Array(m+1).fill(-1);
}
for(let i = 0;i<=m;i++)
{
let temp_ans = maxSubsequenceSubstring(X,Y,n,i,dp);
if(temp_ans > maximum_length) maximum_length = temp_ans;
}
document.write("Length for maximum possible Subsequence of string X which is Substring of Y -> ",maximum_length);
</script>
|
OutputLength for maximum possible Subsequence of string X which is Substring of Y -> 3
Time Complexity: O(n*m) (It will be definitely better than the recursion solution, the worst case is possible only possible when none of the char of string X is there in String Y.)
Space Complexity: O(n*m + n) (the Size of Dp array and stack call size of recursion)
Submethod 2: Tabulation
Let n be length of X and m be length of Y. Create a 2D array ‘dp[][]’ of m + 1 rows and n + 1 columns. Value dp[i][j] is maximum length of subsequence of X[0….j] which is substring of Y[0….i]. Now for each cell of dp[][] fill value as :
for (i = 1 to m)
for (j = 1 to n)
if (x[j-1] == y[i - 1])
dp[i][j] = dp[i-1][j-1] + 1;
else
dp[i][j] = dp[i][j-1];
And finally, the length of the longest subsequence of x which is substring of y is max(dp[i][n]) where 1 <= i <= m.
Below is implementing this approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1000;
int maxSubsequenceSubstring(string x,string y,int n,int m)
{
vector<vector<int>>dp(MAX,vector<int>(MAX,0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (x[j - 1] == y[i - 1])
dp[i][j] = 1 + dp[i - 1][j - 1];
else
dp[i][j] = dp[i][j - 1];
}
}
int ans = 0;
for (int i = 1; i <= m; i++)
ans = max(ans, dp[i][n]);
return ans;
}
int main()
{
string x = "ABCD";
string y = "BACDBDCD";
int n = x.length(), m = y.length();
cout<<maxSubsequenceSubstring(x, y, n, m);
}
|
Java
public class GFG
{
static final int MAX = 1000;
static int maxSubsequenceSubstring(char x[], char y[],
int n, int m)
{
int dp[][] = new int[MAX][MAX];
for (int i = 0; i <= m; i++)
for (int j = 0; j <= n; j++)
dp[i][j] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (x[j - 1] == y[i - 1])
dp[i][j] = 1 + dp[i - 1][j - 1];
else
dp[i][j] = dp[i][j - 1];
}
}
int ans = 0;
for (int i = 1; i <= m; i++)
ans = Math.max(ans, dp[i][n]);
return ans;
}
public static void main(String[] args)
{
char x[] = "ABCD".toCharArray();
char y[] = "BACDBDCD".toCharArray();
int n = x.length, m = y.length;
System.out.println(maxSubsequenceSubstring(x, y, n, m));
}
}
|
Python3
MAX = 1000
def maxSubsequenceSubstring(x, y, n, m):
dp = [[0 for i in range(MAX)]
for i in range(MAX)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if(x[j - 1] == y[i - 1]):
dp[i][j] = 1 + dp[i - 1][j - 1]
else:
dp[i][j] = dp[i][j - 1]
ans = 0
for i in range(1, m + 1):
ans = max(ans, dp[i][n])
return ans
x = "ABCD"
y = "BACDBDCD"
n = len(x)
m = len(y)
print(maxSubsequenceSubstring(x, y, n, m))
|
C#
using System;
public class GFG
{
static int MAX = 1000;
static int maxSubsequenceSubstring(string x, string y,
int n, int m)
{
int[ ,]dp = new int[MAX, MAX];
for (int i = 0; i <= m; i++)
for (int j = 0; j <= n; j++)
dp[i, j] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (x[j - 1] == y[i - 1])
dp[i, j] = 1 + dp[i - 1, j - 1];
else
dp[i, j] = dp[i, j - 1];
}
}
int ans = 0;
for (int i = 1; i <= m; i++)
ans = Math.Max(ans, dp[i,n]);
return ans;
}
public static void Main()
{
string x = "ABCD";
string y = "BACDBDCD";
int n = x.Length, m = y.Length;
Console.WriteLine(maxSubsequenceSubstring(x,
y, n, m));
}
}
|
PHP
<?php
function maxSubsequenceSubstring($x, $y,
$n, $m)
{
$dp;
for ($i = 0; $i <= $m; $i++)
for ($j = 0; $j <= $n; $j++)
$dp[$i][$j] = 0;
for ($i = 1; $i <= $m; $i++) {
for ( $j = 1; $j <= $n; $j++) {
if ($x[$j - 1] == $y[$i - 1])
$dp[$i][$j] = 1 + $dp[$i - 1][$j - 1];
else
$dp[$i][$j] = $dp[$i][$j - 1];
}
}
$ans = 0;
for ( $i = 1; $i <= $m; $i++)
$ans = max($ans, $dp[$i][$n]);
return $ans;
}
{
$x = "ABCD";
$y = "BACDBDCD";
$n = strlen($x); $m = strlen($y);
echo maxSubsequenceSubstring($x, $y, $n, $m);
return 0;
}
?>
|
Javascript
<script>
var MAX = 1000;
function maxSubsequenceSubstring(x, y, n, m)
{
var dp = Array.from(Array(MAX), ()=> Array(MAX));
for (var i = 0; i <= m; i++)
for (var j = 0; j <= n; j++)
dp[i][j] = 0;
for (var i = 1; i <= m; i++) {
for (var j = 1; j <= n; j++) {
if (x[j - 1] == y[i - 1])
dp[i][j] = 1 + dp[i - 1][j - 1];
else
dp[i][j] = dp[i][j - 1];
}
}
var ans = 0;
for (var i = 1; i <= m; i++)
ans = Math.max(ans, dp[i][n]);
return ans;
}
var x = "ABCD";
var y = "BACDBDCD";
var n = x.length, m = y.length;
document.write( maxSubsequenceSubstring(x, y, n, m));
</script>
|
Time Complexity: O(n*m) (Time required to fill the Dp array)
Space Complexity: O(n*m + n) (the Size of Dp array)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...