Find Corners of Rectangle using mid points

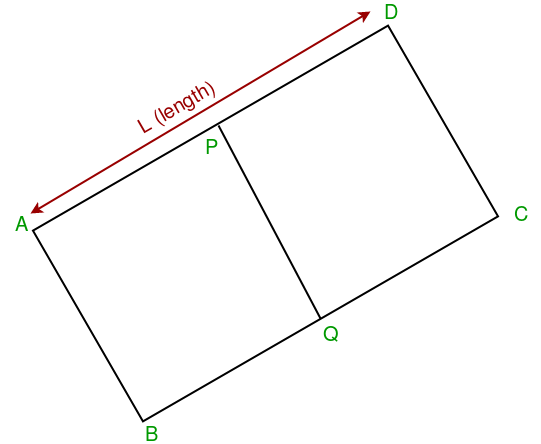
Consider a rectangle ABCD, we’re given the co-ordinates of the mid points of side AD and BC (p and q respectively) along with their length L (AD = BC = L). Now given the parameters, we need to print the co-ordinates of the 4 points A, B, C and D.

Examples: 

Input : p = (1, 0)
        q = (1, 2)
        L = 2
Output : (0, 0), (0, 2), (2, 2), (2, 0)
Explanation:
The printed points form a rectangle which
satisfy the input constraints.

Input : p = (1, 1)
        q = (-1, -1)
        L = 2*sqrt(2)
Output : (0, 2), (-2, 0), (0, -2), (2, 0)

From the problem statement 3 cases can arise :  

1. The Rectangle is horizontal i.e., AD and BC are parallel to X-axis
2. The Rectangle is vertical i.e., AD and BC are parallel to Y-axis
3. The Rectangle is inclined at a certain angle with the axes

The first two cases are trivial and can easily be solved using basic geometry. For the third case we need to apply some mathematical concepts to find the points.

Consider the above diagram for clarity. We have the co-ordinates of p and q. Thus we can find the slope of AD and BC (As pq is perpendicular to AD). Once we have the slope of AD, we can find the equation of straight line passing through AD. Now we can apply distance formula to obtain the displacements along X and Y axes.  

If slope of AD = m, then
m = (p.x- q.x)/(q.y - p.y)

and displacement along X axis, dx =  
   L/(2*sqrt(1+m*m))

Similarly, dy = m*L/(2*sqrt(1+m*m))

Now we can simply find the co-ordinates of 4 corners by simply adding and subtracting the displacements obtained accordingly. 

Below is the implementation .  

C++

// C++ program to find corner points of
// a rectangle using given length and middle
// points.
#include <bits/stdc++.h>
using namespace std;

// Structure to represent a co-ordinate point
struct Point
{
    float x, y;
    Point()
    {
        x = y = 0;
    }
    Point(float a, float b)
    {
        x = a, y = b;
    }
};

// This function receives two points and length
// of the side of rectangle and prints the 4
// corner points of the rectangle
void printCorners(Point p, Point q, float l)
{
    Point a, b, c, d;

    // horizontal rectangle
    if (p.x == q.x)
    {
        a.x = p.x - (l/2.0);
        a.y = p.y;

        d.x = p.x + (l/2.0);
        d.y = p.y;

        b.x = q.x - (l/2.0);
        b.y = q.y;

        c.x = q.x + (l/2.0);
        c.y = q.y;
    }

    // vertical rectangle
    else if (p.y == q.y)
    {
        a.y = p.y - (l/2.0);
        a.x = p.x;

        d.y = p.y + (l/2.0);
        d.x = p.x;

        b.y = q.y - (l/2.0);
        b.x = q.x;

        c.y = q.y + (l/2.0);
        c.x = q.x;
    }

    // slanted rectangle
    else
    {
        // calculate slope of the side
        float m = (p.x-q.x)/float(q.y-p.y);

        // calculate displacements along axes
        float dx = (l /sqrt(1+(m*m))) *0.5 ;
        float dy = m*dx;

        a.x = p.x - dx;
        a.y = p.y - dy;

        d.x = p.x + dx;
        d.y = p.y + dy;

        b.x = q.x - dx;
        b.y = q.y - dy;

        c.x = q.x + dx;
        c.y = q.y + dy;
    }

    cout << a.x << ", " << a.y << " n"
         << b.x << ", " << b.y << "n";
         << c.x << ", " << c.y << " n"
         << d.x << ", " << d.y << "nn";
}

// Driver code
int main()
{
    Point p1(1, 0), q1(1, 2);
    printCorners(p1, q1, 2);

    Point p(1, 1), q(-1, -1);
    printCorners(p, q, 2*sqrt(2));

    return 0;
}

Java

// Java program to find corner points of
// a rectangle using given length and middle
// points.

class GFG
{

    // Structure to represent a co-ordinate point
    static class Point
    {

        float x, y;

        Point()
        {
            x = y = 0;
        }

        Point(float a, float b)
        {
            x = a;
            y = b;
        }
    };

    // This function receives two points and length
    // of the side of rectangle and prints the 4
    // corner points of the rectangle
    static void printCorners(Point p, Point q, float l)
    {
        Point a = new Point(), b = new Point(),
                c = new Point(), d = new Point();

        // horizontal rectangle
        if (p.x == q.x)
        {
            a.x = (float) (p.x - (l / 2.0));
            a.y = p.y;

            d.x = (float) (p.x + (l / 2.0));
            d.y = p.y;

            b.x = (float) (q.x - (l / 2.0));
            b.y = q.y;

            c.x = (float) (q.x + (l / 2.0));
            c.y = q.y;
        }
        // vertical rectangle
        else if (p.y == q.y)
        {
            a.y = (float) (p.y - (l / 2.0));
            a.x = p.x;

            d.y = (float) (p.y + (l / 2.0));
            d.x = p.x;

            b.y = (float) (q.y - (l / 2.0));
            b.x = q.x;

            c.y = (float) (q.y + (l / 2.0));
            c.x = q.x;
        }
        // slanted rectangle
        else
        {
            // calculate slope of the side
            float m = (p.x - q.x) / (q.y - p.y);

            // calculate displacements along axes
            float dx = (float) ((l / Math.sqrt(1 + (m * m))) * 0.5);
            float dy = m * dx;

            a.x = p.x - dx;
            a.y = p.y - dy;

            d.x = p.x + dx;
            d.y = p.y + dy;

            b.x = q.x - dx;
            b.y = q.y - dy;

            c.x = q.x + dx;
            c.y = q.y + dy;
        }

        System.out.print((int)a.x + ", " + (int)a.y + " \n"
                + (int)b.x + ", " + (int)b.y + "\n"
                + (int)c.x + ", " + (int)c.y + " \n"
                + (int)d.x + ", " + (int)d.y + "\n");
    }

    // Driver code
    public static void main(String[] args)
    {
        Point p1 = new Point(1, 0), q1 = new Point(1, 2);
        printCorners(p1, q1, 2);

        Point p = new Point(1, 1), q = new Point(-1, -1);
        printCorners(p, q, (float) (2 * Math.sqrt(2)));
    }
}

// This code contributed by Rajput-Ji

Python3

# Python3 program to find corner points of
# a rectangle using given length and middle
# points.
import math

# Structure to represent a co-ordinate point
class Point:

    def __init__(self, a = 0, b = 0):

        self.x = a
        self.y = b

# This function receives two points and length
# of the side of rectangle and prints the 4
# corner points of the rectangle
def printCorners(p, q, l):

    a, b, c, d = Point(), Point(), Point(), Point()

    # Horizontal rectangle
    if (p.x == q.x):
        a.x = p.x - (l / 2.0)
        a.y = p.y

        d.x = p.x + (l / 2.0)
        d.y = p.y

        b.x = q.x - (l / 2.0)
        b.y = q.y

        c.x = q.x + (l / 2.0)
        c.y = q.y

    # Vertical rectangle
    else if (p.y == q.y):
        a.y = p.y - (l / 2.0)
        a.x = p.x

        d.y = p.y + (l / 2.0)
        d.x = p.x

        b.y = q.y - (l / 2.0)
        b.x = q.x

        c.y = q.y + (l / 2.0)
        c.x = q.x

    # Slanted rectangle
    else:

        # Calculate slope of the side
        m = (p.x - q.x) / (q.y - p.y)

        # Calculate displacements along axes
        dx = (l / math.sqrt(1 + (m * m))) * 0.5
        dy = m * dx

        a.x = p.x - dx
        a.y = p.y - dy

        d.x = p.x + dx
        d.y = p.y + dy

        b.x = q.x - dx
        b.y = q.y - dy

        c.x = q.x + dx
        c.y = q.y + dy

    print(int(a.x), ", ", int(a.y), sep = "")
    print(int(b.x), ", ", int(b.y), sep = "")
    print(int(c.x), ", ", int(c.y), sep = "")
    print(int(d.x), ", ", int(d.y), sep = "")
    print()

# Driver code
p1 = Point(1, 0)
q1 = Point(1, 2)
printCorners(p1, q1, 2)

p = Point(1, 1)
q = Point(-1, -1)
printCorners(p, q, 2 * math.sqrt(2))

# This code is contributed by shubhamsingh10

C#

// C# program to find corner points of
// a rectangle using given length and middle
// points.
using System;

class GFG
{

    // Structure to represent a co-ordinate point
    public class Point
    {

        public float x, y;

        public Point()
        {
            x = y = 0;
        }

        public Point(float a, float b)
        {
            x = a;
            y = b;
        }
    };

    // This function receives two points and length
    // of the side of rectangle and prints the 4
    // corner points of the rectangle
    static void printCorners(Point p, Point q, float l)
    {
        Point a = new Point(), b = new Point(),
                c = new Point(), d = new Point();

        // horizontal rectangle
        if (p.x == q.x)
        {
            a.x = (float) (p.x - (l / 2.0));
            a.y = p.y;

            d.x = (float) (p.x + (l / 2.0));
            d.y = p.y;

            b.x = (float) (q.x - (l / 2.0));
            b.y = q.y;

            c.x = (float) (q.x + (l / 2.0));
            c.y = q.y;
        }

        // vertical rectangle
        else if (p.y == q.y)
        {
            a.y = (float) (p.y - (l / 2.0));
            a.x = p.x;

            d.y = (float) (p.y + (l / 2.0));
            d.x = p.x;

            b.y = (float) (q.y - (l / 2.0));
            b.x = q.x;

            c.y = (float) (q.y + (l / 2.0));
            c.x = q.x;
        }

        // slanted rectangle
        else
        {
            // calculate slope of the side
            float m = (p.x - q.x) / (q.y - p.y);

            // calculate displacements along axes
            float dx = (float) ((l / Math.Sqrt(1 + (m * m))) * 0.5);
            float dy = m * dx;

            a.x = p.x - dx;
            a.y = p.y - dy;

            d.x = p.x + dx;
            d.y = p.y + dy;

            b.x = q.x - dx;
            b.y = q.y - dy;

            c.x = q.x + dx;
            c.y = q.y + dy;
        }

        Console.Write((int)a.x + ", " + (int)a.y + " \n"
                + (int)b.x + ", " + (int)b.y + "\n"
                + (int)c.x + ", " + (int)c.y + " \n"
                + (int)d.x + ", " + (int)d.y + "\n");
    }

    // Driver code
    public static void Main(String[] args)
    {
        Point p1 = new Point(1, 0), q1 = new Point(1, 2);
        printCorners(p1, q1, 2);

        Point p = new Point(1, 1), q = new Point(-1, -1);
        printCorners(p, q, (float) (2 * Math.Sqrt(2)));
    }
}

// This code has been contributed by 29AjayKumar

Javascript

<script>
// Javascript program to find corner points of
// a rectangle using given length and middle
// points.

// Structure to represent a co-ordinate point
class Point
{
    constructor(a,b)
    {
        this.x=a;
        this.y=b;
    }
}

// This function receives two points and length
    // of the side of rectangle and prints the 4
    // corner points of the rectangle
function printCorners(p,q,l)
{
    let a = new Point(), b = new Point(),
                c = new Point(), d = new Point();

        // horizontal rectangle
        if (p.x == q.x)
        {
            a.x =  (p.x - (l / 2.0));
            a.y = p.y;

            d.x =  (p.x + (l / 2.0));
            d.y = p.y;

            b.x =  (q.x - (l / 2.0));
            b.y = q.y;

            c.x =  (q.x + (l / 2.0));
            c.y = q.y;
        }
        // vertical rectangle
        else if (p.y == q.y)
        {
            a.y = (p.y - (l / 2.0));
            a.x = p.x;

            d.y = (p.y + (l / 2.0));
            d.x = p.x;

            b.y = (q.y - (l / 2.0));
            b.x = q.x;

            c.y = (q.y + (l / 2.0));
            c.x = q.x;
        }
        // slanted rectangle
        else
        {
            // calculate slope of the side
            let m = (p.x - q.x) / (q.y - p.y);

            // calculate displacements along axes
            let dx =  ((l / Math.sqrt(1 + (m * m))) * 0.5);
            let dy = m * dx;

            a.x = p.x - dx;
            a.y = p.y - dy;

            d.x = p.x + dx;
            d.y = p.y + dy;

            b.x = q.x - dx;
            b.y = q.y - dy;

            c.x = q.x + dx;
            c.y = q.y + dy;
        }

        document.write(a.x + ", " + a.y + " <br>"
                + b.x + ", " + b.y + "<br>"
                + c.x + ", " + c.y + " <br>"
                + d.x + ", " + d.y + "<br>");
}

// Driver code
let p1 = new Point(1, 0), q1 = new Point(1, 2);
printCorners(p1, q1, 2);

let p = new Point(1, 1), q = new Point(-1, -1);
printCorners(p, q,  (2 * Math.sqrt(2)));

// This code is contributed by rag2127
</script>

Output:

0, 0 
0, 2
2, 2 
2, 0

0, 2 
-2, 0
0, -2 
2, 0

Time Complexity: O(1) 
Auxiliary Space: O(1)

Reference:
StackOverflow
This article is contributed by Aarti_Rathi and Ashutosh Kumar 😀 If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.