Count all combinations of coins to make a given value sum (Coin Change II)
Last Updated :
05 Mar, 2024
Given an integer array of coins[ ] of size N representing different types of denominations and an integer sum, the task is to count all combinations of coins to make a given value sum.
Note: Assume that you have an infinite supply of each type of coin.
Examples:
Input: sum = 4, coins[] = {1,2,3},
Output: 4
Explanation: there are four solutions: {1, 1, 1, 1}, {1, 1, 2}, {2, 2}, {1, 3}.
Input: sum = 10, coins[] = {2, 5, 3, 6}
Output: 5
Explanation: There are five solutions:
{2,2,2,2,2}, {2,2,3,3}, {2,2,6}, {2,3,5} and {5,5}.
Count all combinations of coins to make a given value sum using Recursion:
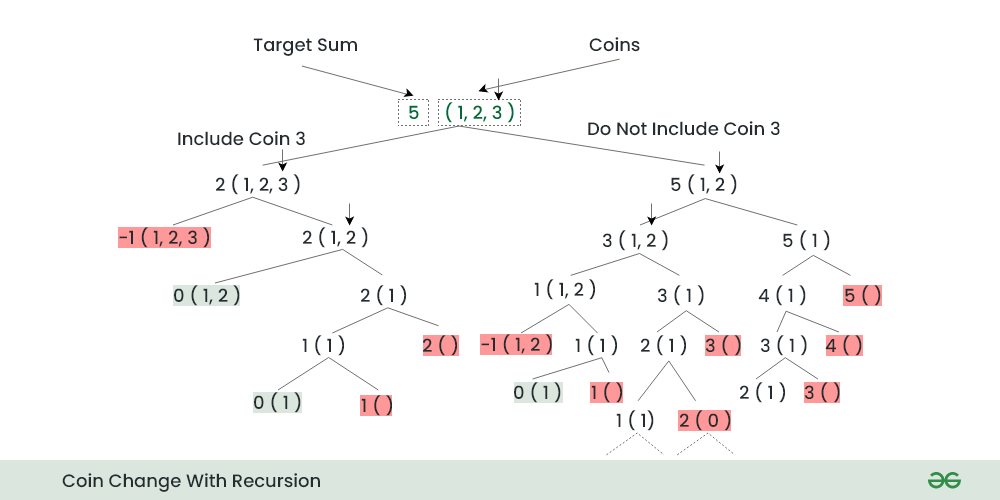
Coin Change Using Recursion
Recurrence Relation:
count(coins,n,sum) = count(coins,n,sum-count[n-1]) + count(coins,n-1,sum)
For each coin, there are 2 options.
- Include the current coin: Subtract the current coin’s denomination from the target sum and call the count function recursively with the updated sum and the same set of coins i.e., count(coins, n, sum – coins[n-1] )
- Exclude the current coin: Call the count function recursively with the same sum and the remaining coins. i.e., count(coins, n-1,sum ).
The final result will be the sum of both cases.
Base case:
- If the target sum (sum) is 0, there is only one way to make the sum, which is by not selecting any coin. So, count(0, coins, n) = 1.
- If the target sum (sum) is negative or no coins are left to consider (n == 0), then there are no ways to make the sum, so count(sum, coins, 0) = 0.
Below is the Implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int count(int coins[], int n, int sum)
{
if (sum == 0)
return 1;
if (sum < 0)
return 0;
if (n <= 0)
return 0;
return count(coins, n, sum - coins[n - 1])
+ count(coins, n - 1, sum);
}
int main()
{
int i, j;
int coins[] = { 1, 2, 3 };
int n = sizeof(coins) / sizeof(coins[0]);
int sum = 5;
cout << " " << count(coins, n, sum);
return 0;
}
|
C
#include <stdio.h>
int count(int coins[], int n, int sum)
{
if (sum == 0)
return 1;
if (sum < 0)
return 0;
if (n <= 0)
return 0;
return count(coins, n - 1, sum)
+ count(coins, n, sum - coins[n - 1]);
}
int main()
{
int i, j;
int coins[] = { 1, 2, 3 };
int n = sizeof(coins) / sizeof(coins[0]);
printf("%d ", count(coins, n, 5));
getchar();
return 0;
}
|
Java
import java.util.*;
class GFG {
static int count(int coins[], int n, int sum)
{
if (sum == 0)
return 1;
if (sum < 0)
return 0;
if (n <= 0)
return 0;
return count(coins, n - 1, sum)
+ count(coins, n, sum - coins[n - 1]);
}
public static void main(String args[])
{
int coins[] = { 1, 2, 3 };
int n = coins.length;
System.out.println(count(coins, n, 5));
}
}
|
C#
using System;
class GFG {
static int count(int[] coins, int n, int sum)
{
if (sum == 0)
return 1;
if (sum < 0)
return 0;
if (n <= 0)
return 0;
return count(coins, n - 1, sum)
+ count(coins, n, sum - coins[n - 1]);
}
public static void Main()
{
int[] coins = { 1, 2, 3 };
int n = coins.Length;
Console.Write(count(coins, n, 5));
}
}
|
Javascript
<script>
function count(coins , n , sum )
{
if (sum == 0)
return 1;
if (sum < 0)
return 0;
if (n <=0)
return 0;
return count( coins, n - 1, sum ) +
count( coins, n, sum - coins[n - 1] );
}
var coins = [1, 2, 3];
var n = coins.length;
document.write( count(coins, n, 5));
</script>
|
PHP
<?php
function coun($coins, $n, $sum)
{
if ($sum == 0)
return 1;
if ($sum < 0)
return 0;
if ($n <= 0)
return 0;
return coun($coins, $n - 1,$sum ) +
coun($coins, $n, $sum - $coins[$n - 1] );
}
$coins = array(1, 2, 3);
$n = count($coins);
echo coun($coins, $n, 5);
?>
|
Python3
def count(coins, n, sum):
if (sum == 0):
return 1
if (sum < 0):
return 0
if (n <= 0):
return 0
return count(coins, n - 1, sum) + count(coins, n, sum-coins[n-1])
coins = [1, 2, 3]
n = len(coins)
print(count(coins, n, 5))
|
Time Complexity: O(2sum)
Auxiliary Space: O(sum)
The above recursive solution has Optimal Substructure and Overlapping Subproblems so Dynamic programming (Memoization) can be used to solve the problem. So 2D array can be used to store results of previously solved subproblems.
Follow the below steps to Implement the idea:
- Create a 2D dp array to store the results of previously solved subproblems.
- dp[i][j] will represent the number of distinct ways to make the sum j by using the first i coins.
- During the recursion call, if the same state is called more than once, then we can directly return the answer stored for that state instead of calculating again.
Below is the implementation using the Memoization:
C++
#include <bits/stdc++.h>
using namespace std;
int count(vector<int>& coins, int n, int sum,
vector<vector<int> >& dp)
{
if (sum == 0)
return dp[n][sum] = 1;
if (n == 0 || sum < 0)
return 0;
if (dp[n][sum] != -1)
return dp[n][sum];
return dp[n][sum]
= count(coins, n, sum - coins[n - 1], dp)
+ count(coins, n - 1, sum, dp);
}
int32_t main()
{
int tc = 1;
while (tc--) {
int n, sum;
n = 3, sum = 5;
vector<int> coins = { 1, 2, 3 };
vector<vector<int> > dp(n + 1,
vector<int>(sum + 1, -1));
int res = count(coins, n, sum, dp);
cout << res << endl;
}
}
|
Java
import java.util.*;
class GFG {
static int count(int[] coins, int sum, int n,
int[][] dp)
{
if (sum == 0)
return dp[n][sum] = 1;
if (n == 0 || sum<0)
return 0;
if (dp[n][sum] != -1)
return dp[n][sum];
return dp[n][sum]
= count(coins, sum - coins[n - 1], n, dp)
+ count(coins, sum, n - 1, dp);
}
public static void main(String[] args)
{
int tc = 1;
while (tc != 0) {
int n, sum;
n = 3;
sum = 5;
int[] coins = { 1, 2, 3 };
int[][] dp = new int[n + 1][sum + 1];
for (int[] row : dp)
Arrays.fill(row, -1);
int res = count(coins, sum, n, dp);
System.out.println(res);
tc--;
}
}
}
|
C#
using System;
public class GFG {
static int count(int[] coins, int sum, int n,
int[, ] dp)
{
if (sum == 0)
return dp[n, sum] = 1;
if (n == 0 || sum < 0)
return 0;
if (dp[n, sum] != -1)
return dp[n, sum];
return dp[n, sum]
= count(coins, sum - coins[n - 1], n, dp)
+ count(coins, sum, n - 1, dp);
}
public static void Main(String[] args)
{
int tc = 1;
while (tc != 0) {
int n, sum;
n = 3;
sum = 5;
int[] coins = { 1, 2, 3 };
int[, ] dp = new int[n + 1, sum + 1];
for (int j = 0; j < n + 1; j++) {
for (int l = 0; l < sum + 1; l++)
dp[j, l] = -1;
}
int res = count(coins, sum, n, dp);
Console.WriteLine(res);
tc--;
}
}
}
|
Javascript
function count(coins , sum , n, dp) {
if (sum == 0)
return dp[n][sum] = 1;
if (n == 0 || sum<0)
return 0;
if (dp[n][sum] != -1)
return dp[n][sum];
return dp[n][sum] = count(coins, sum - coins[n - 1], n, dp) + count(coins, sum, n - 1, dp);
}
var tc = 1;
while (tc != 0) {
var n, sum;
n = 3;
sum = 5;
var coins = [ 1, 2, 3 ];
var dp = Array(n+1).fill().map(() => Array(sum+1).fill(-1));
var res = count(coins, sum, n, dp);
console.log(res);
tc--;
}
|
Python3
def count(coins, sum, n, dp):
if (sum == 0):
dp[n][sum] = 1
return dp[n][sum]
if (n == 0 or sum < 0):
return 0
if (dp[n][sum] != -1):
return dp[n][sum]
dp[n][sum] = count(coins, sum - coins[n - 1], n, dp) + \
count(coins, sum, n - 1, dp)
return dp[n][sum]
if __name__ == '__main__':
tc = 1
while (tc != 0):
n = 3
sum = 5
coins = [1, 2, 3]
dp = [[-1 for i in range(sum+1)] for j in range(n+1)]
res = count(coins, sum, n, dp)
print(res)
tc -= 1
|
Time Complexity: O(N*sum), where N is the number of coins and sum is the target sum.
Auxiliary Space: O(N*sum)
Count all combinations of coins to make a given value sum using Dynamic Programming (Tabulation):
We can use the following steps to implement the dynamic programming(tabulation) approach for Coin Change.
- Create a 2D dp array with rows and columns equal to the number of coin denominations and target sum.
dp[0][0] will be set to 1 which represents the base case where the target sum is 0, and there is only one way to make the change by not selecting any coin.- Iterate through the rows of the dp array (i from 1 to
n), representing the current coin being considered.
- The inner loop iterates over the target sums (
j from 0 to sum).
- Add the number of ways to make change without using the current coin, i.e.,
dp[i][j] += dp[i-1][j].
- Add the number of ways to make change using the current coin, i.e.,
dp[i][j] += dp[i][j-coins[i-1]].
dp[n][sum] will contain the total number of ways to make change for the given target sum using the available coin denominations.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int count(vector<int>& coins, int n, int sum)
{
vector<vector<int> > dp(n + 1, vector<int>(sum + 1, 0));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= sum; j++) {
dp[i][j] += dp[i - 1][j];
if ((j - coins[i - 1]) >= 0) {
dp[i][j] += dp[i][j - coins[i - 1]];
}
}
}
return dp[n][sum];
}
int main()
{
vector<int> coins{ 1, 2, 3 };
int n = 3;
int sum = 5;
cout << count(coins, n, sum);
return 0;
}
|
Java
import java.util.*;
public class CoinChangeWays {
static int count(List<Integer> coins, int n, int sum) {
int[][] dp = new int[n + 1][sum + 1];
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= sum; j++) {
dp[i][j] += dp[i - 1][j];
if ((j - coins.get(i - 1)) >= 0) {
dp[i][j] += dp[i][j - coins.get(i - 1)];
}
}
}
return dp[n][sum];
}
public static void main(String[] args) {
List<Integer> coins = Arrays.asList(1, 2, 3);
int n = 3;
int sum = 5;
System.out.println(count(coins, n, sum));
}
}
|
C#
using System;
using System.Collections.Generic;
class Program {
static int Count(List<int> coins, int n, int sum)
{
int[, ] dp = new int[n + 1, sum + 1];
dp[0, 0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= sum; j++) {
dp[i, j] += dp[i - 1, j];
if ((j - coins[i - 1]) >= 0) {
dp[i, j] += dp[i, j - coins[i - 1]];
}
}
}
return dp[n, sum];
}
static void Main(string[] args)
{
List<int> coins = new List<int>{ 1, 2, 3 };
int n = 3;
int sum = 5;
Console.WriteLine(Count(coins, n, sum));
}
}
|
Javascript
function count(coins, n, sum) {
let dp = new Array(n + 1).fill(0).map(() => new Array(sum + 1).fill(0));
dp[0][0] = 1;
for (let i = 1; i <= n; i++) {
for (let j = 0; j <= sum; j++) {
dp[i][j] += dp[i - 1][j];
if (j - coins[i - 1] >= 0) {
dp[i][j] += dp[i][j - coins[i - 1]];
}
}
}
return dp[n][sum];
}
let coins = [1, 2, 3];
let n = 3;
let sum = 5;
console.log(count(coins, n, sum));
|
Python3
def count(coins, n, target_sum):
dp = [[0 for j in range(target_sum + 1)] for i in range(n + 1)]
dp[0][0] = 1
for i in range(1, n + 1):
for j in range(target_sum + 1):
dp[i][j] += dp[i - 1][j]
if j - coins[i - 1] >= 0:
dp[i][j] += dp[i][j - coins[i - 1]]
return dp[n][target_sum]
if __name__ == "__main__":
coins = [1, 2, 3]
n = 3
target_sum = 5
print(count(coins, n, target_sum))
|
Time complexity : O(N*sum)
Auxiliary Space : O(N*sum)
Count all combinations of coins to make a given value sum Dynamic Programming (Space Optimized):
In the above tabulation approach we are only using dp[i-1][j] and dp[i][j] etc, so we can do space optimization by only using a 1d dp array.
Follow the below steps to Implement the idea:
- Create a 1D dp array,
dp[i] represents the number of ways to make the sum i using the given coin denominations.
- The outer loop iterates over the coins, and the inner loop iterates over the target sums. For each
dp[j], it calculates the number of ways to make change using the current coin denomination and the previous results stored in dp.
dp[sum] contains the total number of ways to make change for the given target sum using the available coin denominations. This approach optimizes space by using a 1D array instead of a 2D DP table.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int count(int coins[], int n, int sum)
{
int dp[sum + 1];
memset(dp, 0, sizeof(dp));
dp[0] = 1;
for (int i = 0; i < n; i++)
for (int j = coins[i]; j <= sum; j++)
dp[j] += dp[j - coins[i]];
return dp[sum];
}
int main()
{
int coins[] = { 1, 2, 3 };
int n = sizeof(coins) / sizeof(coins[0]);
int sum = 5;
cout << count(coins, n, sum);
return 0;
}
|
Java
import java.util.Arrays;
class CoinChange {
static long count(int coins[], int n, int sum)
{
int dp[] = new int[sum + 1];
dp[0] = 1;
for (int i = 0; i < n; i++)
for (int j = coins[i]; j <= sum; j++)
dp[j] += dp[j - coins[i]];
return dp[sum];
}
public static void main(String args[])
{
int coins[] = { 1, 2, 3 };
int n = coins.length;
int sum = 5;
System.out.println(count(coins, n, sum));
}
}
|
Python
def count(coins, n, sum):
dp = [0 for k in range(sum+1)]
dp[0] = 1
for i in range(0, n):
for j in range(coins[i], sum+1):
dp[j] += dp[j-coins[i]]
return dp[sum]
coins = [1, 2, 3]
n = len(coins)
sum = 5
x = count(coins, n, sum)
print(x)
|
C#
using System;
class GFG {
static int count(int[] coins, int n, int sum)
{
int[] dp = new int[sum + 1];
dp[0] = 1;
for (int i = 0; i < n; i++)
for (int j = coins[i]; j <= sum; j++)
dp[j] += dp[j - coins[i]];
return dp[sum];
}
public static void Main()
{
int[] coins = { 1, 2, 3 };
int n = coins.Length;
int sum = 5;
Console.Write(count(coins, n, sum));
}
}
|
Javascript
<script>
function count(coins, n, sum)
{
let dp = new Array(sum + 1);
dp.fill(0);
dp[0] = 1;
for(let i = 0; i < n; i++)
for(let j = coins[i]; j <= sum; j++)
dp[j] += dp[j - coins[i]];
return dp[sum];
}
let coins = [1, 2, 3];
let n = coins.length;
let sum = 4;
document.write(count(coins, n, sum));
</script>
|
PHP
<?php
function count_1( &$coins, $n, $sum )
{
$table = array_fill(0, $sum + 1, NULl);
$table[0] = 1;
for($i = 0; $i < $n; $i++)
for($j = $coins[$i]; $j <= $sum; $j++)
$table[$j] += $table[$j - $coins[$i]];
return $table[$sum];
}
$coins = array(1, 2, 3);
$n = sizeof($coins);
$sum = 4;
$x = count_1($coins, $n, $sum);
echo $x;
?>
|
Time complexity : O(N*sum)
Auxiliary Space : O(sum)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...