Edit Distance
Last Updated :
04 Apr, 2024
Given two strings str1 and str2 of length M and N respectively and below operations that can be performed on str1. Find the minimum number of edits (operations) to convert ‘str1‘ into ‘str2‘.
- Operation 1 (INSERT): Insert any character before or after any index of str1
- Operation 2 (REMOVE): Remove a character of str1
- Operation 3 (Replace): Replace a character at any index of str1 with some other character.
Note: All of the above operations are of equal cost.
Examples:
Input: str1 = “geek”, str2 = “gesek”
Output: 1
Explanation: We can convert str1 into str2 by inserting a ‘s’ between two consecutive ‘e’ in str2.
Input: str1 = “cat”, str2 = “cut”
Output: 1
Explanation: We can convert str1 into str2 by replacing ‘a’ with ‘u’.
Input: str1 = “sunday”, str2 = “saturday”
Output: 3
Explanation: Last three and first characters are same. We basically need to convert “un” to “atur”. This can be done using below three operations. Replace ‘n’ with ‘r’, insert t, insert a
Illustration of Edit Distance:
Let’s suppose we have str1=”GEEXSFRGEEKKS” and str2=”GEEKSFORGEEKS”
Now to convert str1 into str2 we would require 3 minimum operations:
Operation 1: Replace ‘X‘ to ‘K‘
Operation 2: Insert ‘O‘ between ‘F‘ and ‘R‘
Operation 3: Remove second last character i.e. ‘K‘
Refer the below image for better understanding.
-copy.webp)
Edit Distance using Recursion:
Subproblems in Edit Distance:
The idea is to process all characters one by one starting from either from left or right sides of both strings.
Let us process from the right end of the strings, there are two possibilities for every pair of characters being traversed, either they match or they don’t match. If last characters of both string matches then there is no need to perform any operation So, recursively calculate the answer for rest of part of the strings. When last characters do not match, we can perform all three operations to match the last characters in the given strings, i.e. insert, replace, and remove. We then recursively calculate the result for the remaining part of the string. Upon completion of these operations, we will select the minimum answer.
Below is the recursive tree for this problem:
.png)
When the last characters of strings matches. Make a recursive call EditDistance(M-1,N-1) to calculate the answer for remaining part of the strings.
When the last characters of strings don’t matches. Make three recursive calls as show below:
- Insert str1[N-1] at last of str2 : EditDistance(M, N-1)
- Replace str2[M-1] with str1[N-1] : EditDistance(M-1, N-1)
- Remove str2[M-1] : EditDistance(M-1, N)
Recurrence Relations for Edit Distance:
- EditDistance(str1, str2, M, N) = EditDistance(str1, str2, M-1, N-1)
- Case 1: When the last character of both the strings are same
- Case 2: When the last characters are different
- EditDistance(str1, str2, M, N) = 1 + Minimum{ EditDistance(str1, str2 ,M-1,N-1), EditDistance(str1, str2 ,M,N-1), EditDistance(str1, str2 ,M-1,N) }
Base Case for Edit Distance:
- Case 1: When str1 becomes empty i.e. M=0
- return N, as it require N characters to convert an empty string to str1 of size N
- Case 2: When str2 becomes empty i.e. N=0
- return M, as it require M characters to convert an empty string to str2 of size M
Below is the implementation of the above recursive solution.
C++
// A Naive recursive C++ program to find minimum number
// operations to convert str1 to str2
#include <bits/stdc++.h>
using namespace std;
// Utility function to find minimum of three numbers
int min(int x, int y, int z) { return min(min(x, y), z); }
int editDist(string str1, string str2, int m, int n)
{
// If first string is empty, the only option is to
// insert all characters of second string into first
if (m == 0)
return n;
// If second string is empty, the only option is to
// remove all characters of first string
if (n == 0)
return m;
// If last characters of two strings are same, nothing
// much to do. Get the count for
// remaining strings.
if (str1[m - 1] == str2[n - 1])
return editDist(str1, str2, m - 1, n - 1);
// If last characters are not same, consider all three
// operations on last character of first string,
// recursively compute minimum cost for all three
// operations and take minimum of three values.
return 1
+ min(editDist(str1, str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1,
n - 1) // Replace
);
}
// Driver code
int main()
{
// your code goes here
string str1 = "GEEXSFRGEEKKS";
string str2 = "GEEKSFORGEEKS";
cout << editDist(str1, str2, str1.length(),
str2.length());
return 0;
}
// A Naive recursive C program to find minimum number
// operations to convert str1 to str2
#include <stdio.h>
#include <string.h>
// Utility function to find minimum of three numbers
int min(int x, int y, int z)
{
return x < y ? (x < z ? x : z) : (y < z ? y : z);
}
int editDist(char* str1, char* str2, int m, int n)
{
// If first string is empty, the only option is to
// insert all characters of second string into first
if (m == 0)
return n;
// If second string is empty, the only option is to
// remove all characters of first string
if (n == 0)
return m;
// If last characters of two strings are same, nothing
// much to do. Get the count for
// remaining strings.
if (str1[m - 1] == str2[n - 1])
return editDist(str1, str2, m - 1, n - 1);
// If last characters are not same, consider all three
// operations on last character of first string,
// recursively compute minimum cost for all three
// operations and take minimum of three values.
return 1
+ min(
editDist(str1, str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1, n - 1) // Replace
);
}
// Driver code
int main()
{
// your code goes here
char str1[] = "GEEXSFRGEEKKS";
char str2[] = "GEEKSFORGEEKS";
int m = strlen(str1);
int n = strlen(str2);
printf("%d", editDist(str1, str2, m, n));
return 0;
}
// A Naive recursive Java program to find minimum number
// operations to convert str1 to str2
class EDIST {
static int min(int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDist(String str1, String str2, int m,
int n)
{
// If first string is empty, the only option is to
// insert all characters of second string into first
if (m == 0)
return n;
// If second string is empty, the only option is to
// remove all characters of first string
if (n == 0)
return m;
// If last characters of two strings are same,
// nothing much to do. Get the count for remaining
// strings.
if (str1.charAt(m - 1) == str2.charAt(n - 1))
return editDist(str1, str2, m - 1, n - 1);
// If last characters are not same, consider all
// three operations on last character of first
// string, recursively compute minimum cost for all
// three operations and take minimum of three
// values.
return 1
+ min(editDist(str1, str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1,
n - 1) // Replace
);
}
// Driver Code
public static void main(String args[])
{
String str1 = "GEEXSFRGEEKKS";
String str2 = "GEEKSFORGEEKS";
System.out.println(editDist(
str1, str2, str1.length(), str2.length()));
}
}
# A Naive recursive Python program to find minimum number
# operations to convert str1 to str2
def editDistance(str1, str2, m, n):
# If first string is empty, the only option is to
# insert all characters of second string into first
if m == 0:
return n
# If second string is empty, the only option is to
# remove all characters of first string
if n == 0:
return m
# If last characters of two strings are same, nothing
# much to do. Ignore last characters and get count for
# remaining strings.
if str1[m-1] == str2[n-1]:
return editDistance(str1, str2, m-1, n-1)
# If last characters are not same, consider all three
# operations on last character of first string, recursively
# compute minimum cost for all three operations and take
# minimum of three values.
return 1 + min(editDistance(str1, str2, m, n-1), # Insert
editDistance(str1, str2, m-1, n), # Remove
editDistance(str1, str2, m-1, n-1) # Replace
)
# Driver code
str1 = "GEEXSFRGEEKKS"
str2 = "GEEKSFORGEEKS"
print(editDistance(str1, str2, len(str1), len(str2)))
// A Naive recursive C# program to
// find minimum numberoperations
// to convert str1 to str2
using System;
class GFG {
static int min(int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDist(String str1, String str2, int m,
int n)
{
// If first string is empty, the only option is to
// insert all characters of second string into first
if (m == 0)
return n;
// If second string is empty, the only option is to
// remove all characters of first string
if (n == 0)
return m;
// If last characters of two strings are same,
// nothing much to do.Get the count for remaining
// strings.
if (str1[m - 1] == str2[n - 1])
return editDist(str1, str2, m - 1, n - 1);
// If last characters are not same, consider all
// three operations on last character of first
// string, recursively compute minimum cost for all
// three operations and take minimum of three
// values.
return 1
+ min(editDist(str1, str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1,
n - 1) // Replace
);
}
// Driver code
public static void Main()
{
String str1 = "GEEXSFRGEEKKS";
String str2 = "GEEKSFORGEEKS";
Console.WriteLine(
editDist(str1, str2, str1.Length, str2.Length));
}
}
// Javascript program to
// find minimum numberoperations
// to convert str1 to str2
function min(x, y, z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
function editDist(str1, str2, m, n)
{
// If first string is empty, the
// only option is to insert all
// characters of second string into first
if (m == 0)
return n;
// If second string is empty, the only
// option is to remove all characters
// of first string
if (n == 0)
return m;
// If last characters of two strings are
// same, nothing much to do. Get the count for remaining
// strings.
if (str1[m - 1] == str2[n - 1])
return editDist(str1, str2, m - 1, n - 1);
// If last characters are not same, consider all
// three operations on last character of first
// string, recursively compute minimum cost for all
// three operations and take minimum of three
// values.
return 1 +
min(editDist(str1, str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1, n - 1)); // Replace
}
// Driver code
let str1 = "GEEXSFRGEEKKS";
let str2 = "GEEKSFORGEEKS";
console.log(editDist(str1, str2, str1.length,
str2.length));
Time Complexity: O(3^m), when length of “str1” >= length of “str2” and O(3^n), when length of “str2” > length of “str1”. Here m=length of “str1 and n=length of “str2”
Auxiliary Space: O(m), when length of “str1” >= length of “str2” and O(n), when length of “str2” > length of “str1”. Here m=length of “str1 and n=length of “str2”
Edit Distance Using Dynamic Programming (Memoization):
In the above recursive approach, there are several overlapping subproblems:
Edit_Distance(M-1, N-1) is called Three times
Edit_Distance(M-1, N-2) is called Two times
Edit_Distance(M-2, N-1) is called Two times. And so on…
So, we can use Memoization technique to store the result of each subproblems to avoid recalculating the result again and again.
Below are the illustration of overlapping subproblems during the recursion.
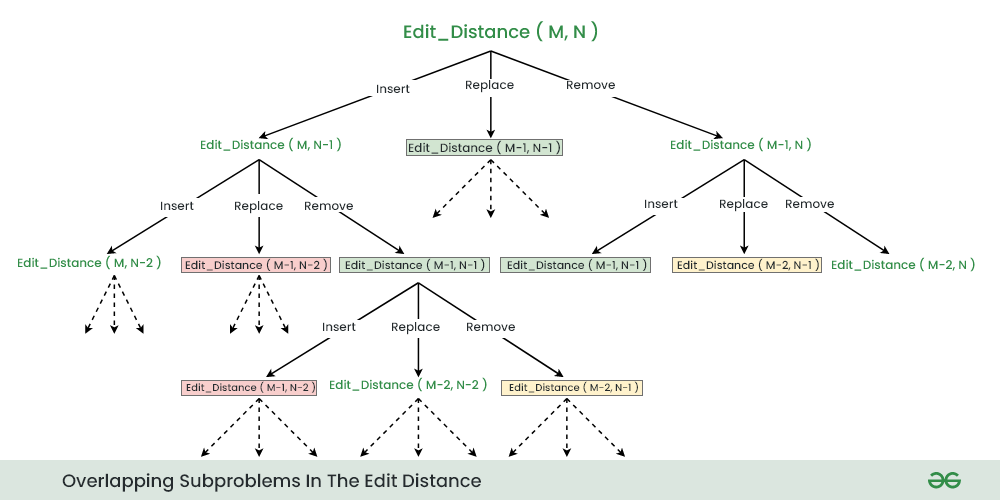
Below is the implementation of Edit Distance Using Dynamic Programming (Memoization):
C++
#include <bits/stdc++.h>
using namespace std;
int minDis(string s1, string s2, int n, int m,
vector<vector<int> >& dp)
{
// If any string is empty,
// return the remaining characters of other string
if (n == 0)
return m;
if (m == 0)
return n;
// To check if the recursive tree
// for given n & m has already been executed
if (dp[n][m] != -1)
return dp[n][m];
// If characters are equal, execute
// recursive function for n-1, m-1
if (s1[n - 1] == s2[m - 1]) {
return dp[n][m] = minDis(s1, s2, n - 1, m - 1, dp);
}
// If characters are nt equal, we need to
// find the minimum cost out of all 3 operations.
// 1. insert 2.delete 3.replace
else {
int insert, del, replace; // temp variables
insert = minDis(s1, s2, n, m - 1, dp);
del = minDis(s1, s2, n - 1, m, dp);
replace = minDis(s1, s2, n - 1, m - 1, dp);
return dp[n][m]
= 1 + min(insert, min(del, replace));
}
}
// Driver program
int main()
{
string str1 = "GEEXSFRGEEKKS";
string str2 = "GEEKSFORGEEKS";
int n = str1.length(), m = str2.length();
vector<vector<int> > dp(n + 1, vector<int>(m + 1, -1));
cout << minDis(str1, str2, n, m, dp);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int min(int x, int y, int z)
{
if (x < y && x < z)
return x;
else if (y < x && y < z)
return y;
else
return z;
}
int minDis(char* s1, char* s2, int n, int m)
{
int dp[n + 1][m + 1];
// Fill dp[][] table in bottom up manner
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
// If first string is empty, only option is to
// insert all characters of second string
if (i == 0)
dp[i][j] = j;
// If second string is empty, only option is to
// remove all characters of second string
else if (j == 0)
dp[i][j] = i;
// If last characters are same, ignore last char
// and recur for remaining string
else if (s1[i - 1] == s2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
// If last character are different, consider all
// possibilities and find minimum
else
dp[i][j]
= 1
+ min(dp[i][j - 1], // Insert
dp[i - 1][j], // Remove
dp[i - 1][j - 1]); // Replace
}
}
return dp[n][m];
}
int main()
{
char* str1 = "GEEXSFRGEEKKS";
char* str2 = "GEEKSFORGEEKS";
int n = strlen(str1), m = strlen(str2);
printf("%d", minDis(str1, str2, n, m));
return 0;
}
import java.util.*;
class GFG {
static int minDis(String s1, String s2, int n, int m,
int[][] dp)
{
// If any String is empty,
// return the remaining characters of other String
if (n == 0)
return m;
if (m == 0)
return n;
// To check if the recursive tree
// for given n & m has already been executed
if (dp[n][m] != -1)
return dp[n][m];
// If characters are equal, execute
// recursive function for n-1, m-1
if (s1.charAt(n - 1) == s2.charAt(m - 1)) {
return dp[n][m]
= minDis(s1, s2, n - 1, m - 1, dp);
}
// If characters are nt equal, we need to
// find the minimum cost out of all 3 operations.
else {
int insert, del, replace; // temp variables
insert = minDis(s1, s2, n, m - 1, dp);
del = minDis(s1, s2, n - 1, m, dp);
replace = minDis(s1, s2, n - 1, m - 1, dp);
return dp[n][m]
= 1
+ Math.min(insert,
Math.min(del, replace));
}
}
// Driver program
public static void main(String[] args)
{
String str1 = "GEEXSFRGEEKKS";
String str2 = "GEEKSFORGEEKS";
int n = str1.length(), m = str2.length();
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i < n + 1; i++)
Arrays.fill(dp[i], -1);
System.out.print(minDis(str1, str2, n, m, dp));
}
}
def minDis(s1, s2, n, m, dp):
# If any string is empty,
# return the remaining characters of other string
if(n == 0):
return m
if(m == 0):
return n
# To check if the recursive tree
# for given n & m has already been executed
if(dp[n][m] != -1):
return dp[n][m]
# If characters are equal, execute
# recursive function for n-1, m-1
if(s1[n - 1] == s2[m - 1]):
if(dp[n - 1][m - 1] == -1):
dp[n][m] = minDis(s1, s2, n - 1, m - 1, dp)
return dp[n][m]
else:
dp[n][m] = dp[n - 1][m - 1]
return dp[n][m]
# If characters are nt equal, we need to
# find the minimum cost out of all 3 operations.
else:
if(dp[n - 1][m] != -1):
m1 = dp[n - 1][m]
else:
m1 = minDis(s1, s2, n - 1, m, dp)
if(dp[n][m - 1] != -1):
m2 = dp[n][m - 1]
else:
m2 = minDis(s1, s2, n, m - 1, dp)
if(dp[n - 1][m - 1] != -1):
m3 = dp[n - 1][m - 1]
else:
m3 = minDis(s1, s2, n - 1, m - 1, dp)
dp[n][m] = 1 + min(m1, min(m2, m3))
return dp[n][m]
# Driver code
str1 = "GEEXSFRGEEKKS"
str2 = "GEEKSFORGEEKS"
n = len(str1)
m = len(str2)
dp = [[-1 for i in range(m + 1)] for j in range(n + 1)]
print(minDis(str1, str2, n, m, dp))
using System;
using System.Collections.Generic;
class GFG {
static int minDis(string s1, string s2, int n, int m,
List<List<int> > dp)
{
// If any string is empty,
// return the remaining characters of other string
if (n == 0)
return m;
if (m == 0)
return n;
// To check if the recursive tree
// for given n & m has already been executed
if (dp[n][m] != -1)
return dp[n][m];
// If characters are equal, execute
// recursive function for n-1, m-1
if (s1[n - 1] == s2[m - 1]) {
if (dp[n - 1][m - 1] == -1) {
return dp[n][m]
= minDis(s1, s2, n - 1, m - 1, dp);
}
else
return dp[n][m] = dp[n - 1][m - 1];
}
// If characters are nt equal, we need to
// find the minimum cost out of all 3 operations.
else {
int m1, m2, m3; // temp variables
if (dp[n - 1][m] != -1) {
m1 = dp[n - 1][m];
}
else {
m1 = minDis(s1, s2, n - 1, m, dp);
}
if (dp[n][m - 1] != -1) {
m2 = dp[n][m - 1];
}
else {
m2 = minDis(s1, s2, n, m - 1, dp);
}
if (dp[n - 1][m - 1] != -1) {
m3 = dp[n - 1][m - 1];
}
else {
m3 = minDis(s1, s2, n - 1, m - 1, dp);
}
return dp[n][m]
= 1 + Math.Min(m1, Math.Min(m2, m3));
}
}
// Driver code
static void Main()
{
string str1 = "GEEXSFRGEEKKS";
string str2 = "GEEKSFORGEEKS";
int n = str1.Length, m = str2.Length;
List<List<int> > dp = new List<List<int> >();
for (int i = 0; i < n + 1; i++) {
dp.Add(new List<int>());
for (int j = 0; j < m + 1; j++) {
dp[i].Add(-1);
}
}
Console.WriteLine(minDis(str1, str2, n, m, dp));
}
}
function minDis(s1,s2,n,m,dp)
{
// If any String is empty,
// return the remaining characters of other String
if(n == 0)
return m;
if(m == 0)
return n;
// To check if the recursive tree
// for given n & m has already been executed
if(dp[n][m] != -1)
return dp[n][m];
// If characters are equal, execute
// recursive function for n-1, m-1
if(s1[n - 1] == s2[m - 1])
{
if(dp[n - 1][m - 1] == -1)
{
return dp[n][m] = minDis(s1, s2, n - 1, m - 1, dp);
}
else
return dp[n][m] = dp[n - 1][m - 1];
}
// If characters are nt equal, we need to
// find the minimum cost out of all 3 operations.
else
{
let m1, m2, m3; // temp variables
if(dp[n-1][m] != -1)
{
m1 = dp[n - 1][m];
}
else
{
m1 = minDis(s1, s2, n - 1, m, dp);
}
if(dp[n][m - 1] != -1)
{
m2 = dp[n][m - 1];
}
else
{
m2 = minDis(s1, s2, n, m - 1, dp);
}
if(dp[n - 1][m - 1] != -1)
{
m3 = dp[n - 1][m - 1];
}
else
{
m3 = minDis(s1, s2, n - 1, m - 1, dp);
}
return dp[n][m] = 1 + Math.min(m1, Math.min(m2, m3));
}
}
// Driver program
let str1 = "GEEXSFRGEEKKS";
let str2 = "GEEKSFORGEEKS";
let n= str1.length, m = str2.length;
let dp = new Array(n + 1);
for(let i = 0; i < n + 1; i++)
{
dp[i]=new Array(m+1);
for(let j=0;j<m+1;j++)
dp[i][j]=-1;
}
console.log(minDis(str1, str2, n, m, dp));
Time Complexity: O(m x n)
Auxiliary Space: O( m *n)+O(m+n) , (m*n) extra array space and (m+n) recursive stack space.
Edit Distance Using Dynamic Programming (Bottom-Up Approach):
Use a table to store solutions of subproblems to avoiding recalculate the same subproblems multiple times. By doing this, if same subproblems repeated during, we retrieve the solutions from the table itself.
Below are the steps to convert the recursive approach to Bottom up approach:
1. Choosing Dimensions of Table: The state of smaller sub-problems depends on the input parameters m and n because at least one of them will decrease after each recursive call. So we need to construct a 2D table dp[][] to store the solution of the sub-problems.
2. Choosing Correct size of Table: The size of the 2D table will be equal to the total number of different subproblems, which is equal to (m + 1)*(n + 1). As both m and n are decreasing by 1 during the recursive calls and reaching the value 0. So m + 1 possibilities for the first parameter and n + 1 possibilities for the second parameter. Total number of possible subproblems = (m + 1)*(n + 1).
3. Filling the table: It consist of two stages, table initialization and building the solution from the smaller subproblems:
- Table initialization: Before building the solution, we need to initialize the table with the smaller version of the solution i.e. base case. Here m = 0 and n = 0 is the situation of the base case, so we initialize first-column dp[i][0] with i and first-row dp[0][j] with j.
- Building the solution of larger problems from the smaller subproblems: We can easily define the iterative structure by using the recursive structure of the above recursive solution.
- if (str1[i – 1] == str2[j – 1]) dp[i][j] = dp[i – 1][j – 1];
- if (str1[i – 1] != str2[j – 1]) dp[i][j] = 1 + min(dp[i][j – 1], dp[i – 1][j], dp[i – 1][j – 1]);
4. Returning final solution: After filling the table iteratively, our final solution gets stored at the bottom right corner of the 2-D table i.e. we return Edit[m][n] as an output.
Below is the implementation of the above algorithm:
C++
// A Dynamic Programming based C++ program to find minimum
// number operations to convert str1 to str2
#include <bits/stdc++.h>
using namespace std;
// Utility function to find the minimum of three numbers
int min(int x, int y, int z) { return min(min(x, y), z); }
int editDistDP(string str1, string str2, int m, int n)
{
// Create a table to store results of subproblems
int dp[m + 1][n + 1];
// Fill d[][] in bottom up manner
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
// If first string is empty, only option is to
// insert all characters of second string
if (i == 0)
dp[i][j] = j; // Min. operations = j
// If second string is empty, only option is to
// remove all characters of second string
else if (j == 0)
dp[i][j] = i; // Min. operations = i
// If last characters are same, ignore last char
// and recur for remaining string
else if (str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
// If the last character is different, consider
// all possibilities and find the minimum
else
dp[i][j]
= 1
+ min(dp[i][j - 1], // Insert
dp[i - 1][j], // Remove
dp[i - 1][j - 1]); // Replace
}
}
return dp[m][n];
}
// Driver code
int main()
{
// your code goes here
string str1 = "GEEXSFRGEEKKS";
string str2 = "GEEKSFORGEEKS";
cout << editDistDP(str1, str2, str1.length(),
str2.length());
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// Utility function to find the minimum of three numbers
int min(int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
return z;
}
int editDistDP(char* str1, char* str2, int m, int n)
{
// Create a table to store results of subproblems
int dp[m + 1][n + 1];
// Fill d[][] in bottom up manner
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
// If first string is empty, only option is to
// insert all characters of second string
if (i == 0)
dp[i][j] = j; // Min. operations = j
// If second string is empty, only option is to
// remove all characters of second string
else if (j == 0)
dp[i][j] = i; // Min. operations = i
// If last characters are same, ignore last char
// and recur for remaining string
else if (str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
// If the last character is different, consider
// all possibilities and find the minimum
else
dp[i][j]
= 1
+ min(dp[i][j - 1], // Insert
dp[i - 1][j], // Remove
dp[i - 1][j - 1]); // Replace
}
}
return dp[m][n];
}
// Driver code
int main()
{
char str1[] = "GEEXSFRGEEKKS";
char str2[] = "GEEKSFORGEEKS";
int m = strlen(str1);
int n = strlen(str2);
printf("%d\n", editDistDP(str1, str2, m, n));
return 0;
}
// A Dynamic Programming based Java program to find minimum
// number operations to convert str1 to str2
import java.io.*;
class EDIST {
static int min(int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDistDP(String str1, String str2, int m,
int n)
{
// Create a table to store results of subproblems
int dp[][] = new int[m + 1][n + 1];
// Fill d[][] in bottom up manner
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
// If first string is empty, only option is
// to insert all characters of second string
if (i == 0)
dp[i][j] = j; // Min. operations = j
// If second string is empty, only option is
// to remove all characters of second string
else if (j == 0)
dp[i][j] = i; // Min. operations = i
// If last characters are same, ignore last
// char and recur for remaining string
else if (str1.charAt(i - 1)
== str2.charAt(j - 1))
dp[i][j] = dp[i - 1][j - 1];
// If the last character is different,
// consider all possibilities and find the
// minimum
else
dp[i][j]
= 1
+ min(
dp[i][j - 1], // Insert
dp[i - 1][j], // Remove
dp[i - 1][j - 1]); // Replace
}
}
return dp[m][n];
}
// Driver Code
public static void main(String args[])
{
String str1 = "GEEXSFRGEEKKS";
String str2 = "GEEKSFORGEEKS";
System.out.println(editDistDP(
str1, str2, str1.length(), str2.length()));
}
}
# A Dynamic Programming based Python program for edit
# distance problem
def editDistDP(str1, str2, m, n):
# Create a table to store results of subproblems
dp = [[0 for x in range(n + 1)] for x in range(m + 1)]
# Fill d[][] in bottom up manner
for i in range(m + 1):
for j in range(n + 1):
# If first string is empty, only option is to
# insert all characters of second string
if i == 0:
dp[i][j] = j # Min. operations = j
# If second string is empty, only option is to
# remove all characters of second string
elif j == 0:
dp[i][j] = i # Min. operations = i
# If last characters are same, ignore last char
# and recur for remaining string
elif str1[i-1] == str2[j-1]:
dp[i][j] = dp[i-1][j-1]
# If last character are different, consider all
# possibilities and find minimum
else:
dp[i][j] = 1 + min(dp[i][j-1], # Insert
dp[i-1][j], # Remove
dp[i-1][j-1]) # Replace
return dp[m][n]
# Driver code
str1 = "GEEXSFRGEEKKS"
str2 = "GEEKSFORGEEKS"
print(editDistDP(str1, str2, len(str1), len(str2)))
// A Dynamic Programming based
// C# program to find minimum
// number operations to
// convert str1 to str2
using System;
class GFG {
static int min(int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDistDP(String str1, String str2, int m,
int n)
{
// Create a table to store
// results of subproblems
int[, ] dp = new int[m + 1, n + 1];
// Fill d[][] in bottom up manner
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
// If first string is empty, only option is
// to insert all characters of second string
if (i == 0)
// Min. operations = j
dp[i, j] = j;
// If second string is empty, only option is
// to remove all characters of second string
else if (j == 0)
// Min. operations = i
dp[i, j] = i;
// If last characters are same, ignore last
// char and recur for remaining string
else if (str1[i - 1] == str2[j - 1])
dp[i, j] = dp[i - 1, j - 1];
// If the last character is different,
// consider all possibilities and find the
// minimum
else
dp[i, j] = 1
+ min(dp[i, j - 1], // Insert
dp[i - 1, j], // Remove
dp[i - 1,
j - 1]); // Replace
}
}
return dp[m, n];
}
// Driver code
public static void Main()
{
String str1 = "GEEXSFRGEEKKS";
String str2 = "GEEKSFORGEEKS";
Console.Write(editDistDP(str1, str2, str1.Length,
str2.Length));
}
}
// A Dynamic Programming based
// Javascript program to find minimum
// number operations to convert str1 to str2
function min(x,y,z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
function editDistDP(str1,str2,m,n)
{
// Create a table to store results of subproblems
let dp = new Array(m + 1);
for(let i=0;i<m+1;i++)
{
dp[i]=new Array(n+1);
for(let j=0;j<n+1;j++)
{
dp[i][j]=0;
}
}
// Fill d[][] in bottom up manner
for (let i = 0; i <= m; i++) {
for (let j = 0; j <= n; j++) {
// If first string is empty, only option is
// to insert all characters of second string
if (i == 0)
dp[i][j] = j; // Min. operations = j
// If second string is empty, only option is
// to remove all characters of second string
else if (j == 0)
dp[i][j] = i; // Min. operations = i
// If last characters are same, ignore last
// char and recur for remaining string
else if (str1[i - 1]
== str2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
// If the last character is different,
// consider all possibilities and find the
// minimum
else
dp[i][j] = 1
+ min(dp[i][j - 1], // Insert
dp[i - 1][j], // Remove
dp[i - 1]
[j - 1]); // Replace
}
}
return dp[m][n];
}
// Driver Code
let str1 = "GEEXSFRGEEKKS";
let str2 = "GEEKSFORGEEKS";
console.log(editDistDP(str1, str2, str1.length, str2.length));
Time Complexity: O(m x n)
Auxiliary Space: O(m x n)
Edit Distance Using Dynamic Programming (Optimization in Space Complexity):
Optimized Space Complexity Solution: In the above bottom up approach we require O(m x n) space. Let’s take an observation and try to optimize our space complexity:
To fill a row in DP array we require only one row i.e. the upper row. For example, if we are filling the row where i=10 in DP array then we require only values of 9th row. So we simply create a DP array of 2 x str1 length. This approach reduces the space complexity from O(N*M) to O(2*N).
Below is the implementation of the above approach:
C++
// A Space efficient Dynamic Programming
// based C++ program to find minimum
// number operations to convert str1 to str2
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// space optimization
int editDistance(string s, string t)
{
int m = s.size();
int n = t.size();
vector<int> prev(n + 1, 0), curr(n + 1, 0);
for (int j = 0; j <= n; j++) {
prev[j] = j;
}
for (int i = 1; i <= m; i++) {
curr[0] = i;
for (int j = 1; j <= n; j++) {
if (s[i - 1] == t[j - 1]) {
curr[j] = prev[j - 1];
}
else {
int mn
= min(1 + prev[j], 1 + curr[j - 1]);
curr[j] = min(mn, 1 + prev[j - 1]);
}
}
prev = curr;
}
return prev[n];
}
};
int main()
{
string s = "GEEXSFRGEEKKS", t = "GEEKSFORGEEKS";
Solution ob;
int ans = ob.editDistance(s, t);
cout << ans << "\n";
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int min(int a, int b, int c)
{
if (a < b && a < c) {
return a;
}
else if (b < a && b < c) {
return b;
}
else {
return c;
}
}
int editDistance(char* s, char* t)
{
int n = strlen(s);
int m = strlen(t);
int* prev = (int*)calloc(m + 1, sizeof(int));
int* curr = (int*)calloc(m + 1, sizeof(int));
for (int j = 0; j <= m; j++) {
prev[j] = j;
}
for (int i = 1; i <= n; i++) {
curr[0] = i;
for (int j = 1; j <= m; j++) {
if (s[i - 1] == t[j - 1]) {
curr[j] = prev[j - 1];
}
else {
int mn = min(1 + prev[j], 1 + curr[j - 1],
1 + prev[j - 1]);
curr[j] = mn;
}
}
memcpy(prev, curr, (m + 1) * sizeof(int));
}
int ans = prev[m];
free(prev);
free(curr);
return ans;
}
int main()
{
char s[] = "GEEXSFRGEEKKS";
char t[] = "GEEKSFORGEEKS";
int ans = editDistance(s, t);
printf("%d\n", ans);
return 0;
}
// A Space efficient Dynamic Programming
// based Java program to find minimum
// number operations to convert str1 to str2
import java.util.*;
class Solution {
// space optimization
public int editDistance(String s, String t)
{
int n = s.length();
int m = t.length();
int[] prev = new int[m + 1];
int[] curr = new int[m + 1];
for (int j = 0; j <= m; j++) {
prev[j] = j;
}
for (int i = 1; i <= n; i++) {
curr[0] = i;
for (int j = 1; j <= m; j++) {
if (s.charAt(i - 1) == t.charAt(j - 1)) {
curr[j] = prev[j - 1];
}
else {
int mn = Math.min(1 + prev[j],
1 + curr[j - 1]);
curr[j] = Math.min(mn, 1 + prev[j - 1]);
}
}
prev = curr.clone();
}
return prev[m];
}
}
public class Main {
public static void main(String[] args)
{
String s = "GEEXSFRGEEKKS";
String t = "GEEKSFORGEEKS";
Solution ob = new Solution();
int ans = ob.editDistance(s, t);
System.out.println(ans);
}
}
# A Space efficient Dynamic Programming
# based Python3 program to find minimum
# number operations to convert str1 to str2
class Solution:
def editDistance(self, s: str, t: str) -> int:
n = len(s)
m = len(t)
prev = [j for j in range(m+1)]
curr = [0] * (m+1)
for i in range(1, n+1):
curr[0] = i
for j in range(1, m+1):
if s[i-1] == t[j-1]:
curr[j] = prev[j-1]
else:
mn = min(1 + prev[j], 1 + curr[j-1])
curr[j] = min(mn, 1 + prev[j-1])
prev = curr.copy()
return prev[m]
s = "GEEXSFRGEEKKS"
t = "GEEKSFORGEEKS"
ob = Solution()
ans = ob.editDistance(s, t)
print(ans)
using System;
using System.Collections.Generic;
class Solution {
public int EditDistance(string s, string t)
{
int n = s.Length;
int m = t.Length;
List<int> prev = new List<int>();
List<int> curr = new List<int>();
for (int j = 0; j <= m; j++) {
prev.Add(j);
}
for (int i = 1; i <= n; i++) {
curr.Add(i);
for (int j = 1; j <= m; j++) {
if (s[i - 1] == t[j - 1]) {
curr.Add(prev[j - 1]);
}
else {
int mn = Math.Min(1 + prev[j],
1 + curr[j - 1]);
curr.Add(Math.Min(mn, 1 + prev[j - 1]));
}
}
prev = new List<int>(curr);
curr.Clear();
}
return prev[m];
}
}
class Program {
static void Main(string[] args)
{
string s = "GEEXSFRGEEKKS";
string t = "GEEKSFORGEEKS";
Solution ob = new Solution();
int ans = ob.EditDistance(s, t);
Console.WriteLine(ans);
}
}
class Solution {
// space optimization
editDistance(s, t) {
const n = s.length;
const m = t.length;
const prev = new Array(m + 1).fill(0);
const curr = new Array(m + 1).fill(0);
for (let j = 0; j <= m; j++) {
prev[j] = j;
}
for (let i = 1; i <= n; i++) {
curr[0] = i;
for (let j = 1; j <= m; j++) {
if (s[i - 1] === t[j - 1]) {
curr[j] = prev[j - 1];
} else {
const mn = Math.min(1 + prev[j], 1 + curr[j - 1]);
curr[j] = Math.min(mn, 1 + prev[j - 1]);
}
}
prev.splice(0, m + 1, ...curr);
}
return prev[m];
}
}
const s = "GEEXSFRGEEKKS";
const t = "GEEKSFPRGEEKS";
const ob = new Solution();
const ans = ob.editDistance(s, t);
console.log(ans);
Time Complexity: O(M x N) where M and N are lengths of the string
Auxiliary Space: O( N ), Length of the str2
Edit Distance Using Dynamic Programming (Further Optimization in Space Complexity):
As discussed the above approach uses two 1-D arrays, now the question is can we achieve our task by using only a single 1-D array?
The answer is Yes and it requires a simple observation as mentioned below:
In the previous approach The curr[] array is updated using 3 values only :
Value 1: curr[j] = prev[j-1] when str1[i-1] is equal to str2[j-1]
Value 2: curr[j] = prev[j] when str1[i-1] is not equal to str2[j-1]
Value 3: curr[j] = curr[j-1] when str1[i-1] is not equal to str2[j-1]
By keeping the track of these three values we can achiever our task using only a single 1-D array
Below is the code implementation of the approach:
C++
// A Space efficient Dynamic Programming
// based C++ program to find minimum
// number operations to convert str1 to str2
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// space optimization
int editDistance(string str1, string str2)
{
int m = str1.size();
int n = str2.size();
int previous;
vector<int> curr(n + 1, 0);
for (int j = 0; j <= n; j++) {
curr[j] = j;
}
for (int i = 1; i <= m; i++) {
previous = curr[0];
curr[0] = i;
for (int j = 1; j <= n; j++) {
int temp = curr[j];
if (str1[i - 1] == str2[j - 1]) {
curr[j] = previous;
}
else {
curr[j] = 1
+ min({ previous, curr[j - 1],
curr[j] });
}
previous = temp;
}
}
return curr[n];
}
};
int main()
{
string str1 = "GEEXSFRGEEKKS", str2 = "GEEKSFORGEEKS";
Solution ob;
int ans = ob.editDistance(str1, str2);
cout << ans << "\n";
return 0;
}
public class EditDistance {
// This method calculates the edit distance (Levenshtein
// distance) between two strings.
public int editDistance(String str1, String str2)
{
// Get the lengths of the two input strings.
int m = str1.length();
int n = str2.length();
// Initialize an array to store the current row of
// edit distances.
int[] curr = new int[n + 1];
// Initialize the first row with values 0 to n.
for (int j = 0; j <= n; j++) {
curr[j] = j;
}
int previous;
for (int i = 1; i <= m; i++) {
// Store the value of the previous row's first
// column.
previous = curr[0];
curr[0] = i;
for (int j = 1; j <= n; j++) {
// Store the current value before updating
// it.
int temp = curr[j];
// Check if the characters at the current
// positions in str1 and str2 are the same.
if (str1.charAt(i - 1)
== str2.charAt(j - 1)) {
// If they are the same, no additional
// cost is incurred.
curr[j] = previous;
}
else {
// If the characters are different,
// calculate the minimum of three
// operations:
// 1. Deletion (previous value)
// 2. Insertion (current row's previous
// value)
// 3. Substitution (diagonal previous
// value)
curr[j] = 1 + Math.min(
Math.min(previous, curr[j - 1]), curr[j]);
}
// Update the previous value to the stored
// temporary value.
previous = temp;
}
}
// The value in the last cell of the current row
// represents the edit distance.
return curr[n];
}
public static void main(String[] args)
{
String str1 = "GEEXSFRGEEKKS";
String str2 = "GEEKSFORGEEKS";
EditDistance ed = new EditDistance();
int ans = ed.editDistance(str1, str2);
System.out.println(ans);
}
}
def editDistance(str1, str2):
# Get the lengths of the input strings
m = len(str1)
n = len(str2)
# Initialize a list to store the current row
curr = [0] * (n + 1)
# Initialize the first row with values from 0 to n
for j in range(n + 1):
curr[j] = j
# Initialize a variable to store the previous value
previous = 0
# Loop through the rows of the dynamic programming matrix
for i in range(1, m + 1):
# Store the current value at the beginning of the row
previous = curr[0]
curr[0] = i
# Loop through the columns of the dynamic programming matrix
for j in range(1, n + 1):
# Store the current value in a temporary variable
temp = curr[j]
# Check if the characters at the current positions in str1 and str2 are the same
if str1[i - 1] == str2[j - 1]:
curr[j] = previous
else:
# Update the current cell with the minimum of the three adjacent cells
curr[j] = 1 + min(previous, curr[j - 1], curr[j])
# Update the previous variable with the temporary value
previous = temp
# The value in the last cell represents the minimum number of operations
return curr[n]
# Driver Code
if __name__ == "__main__":
str1 = "GEEXSFRGEEKKS"
str2 = "GEEKSFORGEEKS"
ans = editDistance(str1, str2)
print(ans)
using System;
class GFG {
// Function to calculate the minimum edit distance
// between two strings
static int EditDistance(string str1, string str2)
{
// Get the length of the first string
int m = str1.Length;
// Get the length of the second string
int n = str2.Length;
// Initialize an array to store the current row
int[] curr = new int[n + 1];
for (int j = 0; j <= n; j++) {
// Initialize the first row with values from 0
// to n
curr[j] = j;
}
// Initialize a variable to store the previous value
int previous = 0;
for (int i = 1; i <= m; i++) {
// Store the current value at the beginning of
// the row
previous = curr[0];
// Update the first element of the current row
curr[0] = i;
for (int j = 1; j <= n; j++) {
// Store the current value in a temporary
// variable
int temp = curr[j];
if (str1[i - 1] == str2[j - 1]) {
// Characters are the same, no operation
// needed
curr[j] = previous;
}
else {
// Update the current cell with the
// minimum of the three adjacent cells
curr[j]
= 1
+ Math.Min(previous,
Math.Min(curr[j - 1],
curr[j]));
}
// Update the previous variable with the
// temporary value
previous = temp;
}
}
// The value in the last cell represents the minimum
// number of operations
return curr[n];
}
// Driver Code
static void Main(string[] args)
{
string str1 = "GEEXSFRGEEKKS";
string str2 = "GEEKSFORGEEKS";
// Calculate the edit distance
int ans = EditDistance(str1, str2);
Console.WriteLine(ans);
}
}
function editDistance(str1, str2) {
// Get the lengths of the input strings
const m = str1.length;
const n = str2.length;
// Initialize an array to store the current row
const curr = new Array(n + 1).fill(0);
// Initialize the first row with values from 0 to n
for (let j = 0; j <= n; j++) {
curr[j] = j;
}
// Initialize a variable to store the previous value
let previous = 0;
// Loop through the rows of the dynamic programming matrix
for (let i = 1; i <= m; i++) {
// Store the current value at the beginning of the row
previous = curr[0];
curr[0] = i;
// Loop through the columns of the dynamic programming matrix
for (let j = 1; j <= n; j++) {
// Store the current value in a temporary variable
const temp = curr[j];
// Check if the characters at the current positions in str1 and str2 are the same
if (str1[i - 1] === str2[j - 1]) {
curr[j] = previous;
} else {
// Update the current cell with the minimum of the three adjacent cells
curr[j] = 1 + Math.min(previous, curr[j - 1], curr[j]);
}
// Update the previous variable with the temporary value
previous = temp;
}
}
// The value in the last cell represents the minimum number of operations
return curr[n];
}
// Driver Code
const str1 = "GEEXSFRGEEKKS";
const str2 = "GEEKSFORGEEKS";
const ans = editDistance(str1, str2);
console.log(ans);
Time Complexity: O(M*N)
Auxiliary Space: O(N)
Real-World Applications of Edit Distance:
- Spell Checking and Auto-Correction
- DNA Sequence Alignment
- Plagiarism Detection
- Natural Language Processing
- Version Control Systems
- String Matching
https://youtu.be/Thv3TfsZVpw
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...