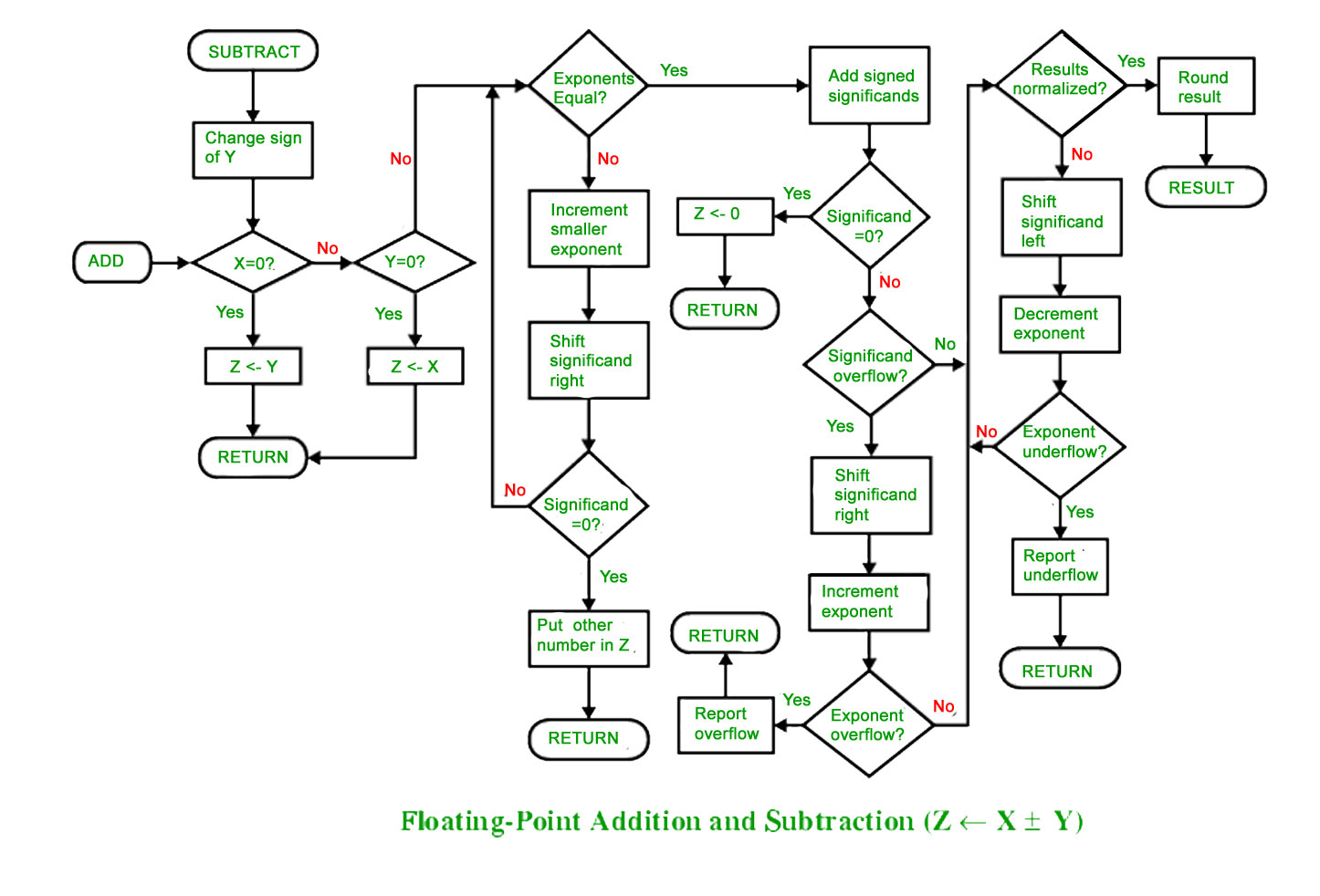
FLOATING POINT ADDITION AND SUBTRACTION
To understand floating point addition, first we see addition of real numbers in decimal as same logic is applied in both cases.
For example, we have to add 1.1 * 103 and 50.
We cannot add these numbers directly. First, we need to align the exponent and then, we can add significant.
After aligning exponent, we get 50 = 0.05 * 103
Now adding significant, 0.05 + 1.1 = 1.15
So, finally we get (1.1 * 103 + 50) = 1.15 * 103
Here, notice that we shifted 50 and made it 0.05 to add these numbers.
Now let us take example of floating point number addition
We follow these steps to add two numbers:
1. Align the significant
2. Add the significant
3. Normalize the result
Let the two numbers be
x = 9.75
y = 0.5625
Converting them into 32-bit floating point representation,
9.75’s representation in 32-bit format = 0 10000010 00111000000000000000000
0.5625’s representation in 32-bit format = 0 01111110 00100000000000000000000
Now we get the difference of exponents to know how much shifting is required.
(10000010 – 01111110)2 = (4)10
Now, we shift the mantissa of lesser number right side by 4 units.
Mantissa of 0.5625 = 1.00100000000000000000000
(note that 1 before decimal point is understood in 32-bit representation)
Shifting right by 4 units, we get 0.00010010000000000000000
Mantissa of 9.75 = 1. 00111000000000000000000
Adding mantissa of both
0. 00010010000000000000000
+ 1. 00111000000000000000000
————————————————-
1. 01001010000000000000000
In final answer, we take exponent of bigger number
So, final answer consist of :
Sign bit = 0
Exponent of bigger number = 10000010
Mantissa = 01001010000000000000000
32 bit representation of answer = x + y = 0 10000010 01001010000000000000000
- FLOATING POINT SUBTRACTION
Subtraction is similar to addition with some differences like we subtract mantissa unlike addition and in sign bit we put the sign of greater number.
Let the two numbers be
x = 9.75
y = – 0.5625
Converting them into 32-bit floating point representation
9.75’s representation in 32-bit format = 0 10000010 00111000000000000000000
– 0.5625’s representation in 32-bit format = 1 01111110 00100000000000000000000
Now, we find the difference of exponents to know how much shifting is required.
(10000010 – 01111110)2 = (4)10
Now, we shift the mantissa of lesser number right side by 4 units.
Mantissa of – 0.5625 = 1.00100000000000000000000
(note that 1 before decimal point is understood in 32-bit representation)
Shifting right by 4 units, 0.00010010000000000000000
Mantissa of 9.75= 1. 00111000000000000000000
Subtracting mantissa of both
0. 00010010000000000000000
– 1. 00111000000000000000000
————————————————
1. 00100110000000000000000
Sign bit of bigger number = 0
So, finally the answer = x – y = 0 10000010 00100110000000000000000
This article has been contributed by Anuj Batham.
In this continuation of the previous set, we will cover some more concepts and operations involved in computer arithmetic:
- Signed vs. unsigned numbers: In computer arithmetic, numbers can be either signed or unsigned. Unsigned numbers only represent positive values, while signed numbers can represent both positive and negative values. Signed numbers are typically represented using two’s complement notation.
- Shift operations: Shift operations are used to move the bits of a number left or right. A left shift multiplies the number by 2 raised to the power of the number of shifted bits, while a right shift divides the number by 2 raised to the power of the number of shifted bits.
- Logical vs. arithmetic shifts: Shift operations can be either logical or arithmetic. Logical shifts insert zeros into the vacant bit positions, while arithmetic shifts preserve the sign bit when shifting a signed number.
- Carry and borrow: In addition and subtraction operations, carry and borrow refer to the bit that is carried over or borrowed from the next digit position when the result of an operation exceeds the number of bits available.
- Boolean algebra: Boolean algebra is a branch of mathematics that deals with logical operations on binary variables. It is widely used in computer arithmetic for operations such as bitwise AND, OR, and XOR.
- Fixed-point arithmetic: Fixed-point arithmetic is used to perform arithmetic operations on numbers with a fixed number of decimal places. It is commonly used in applications such as digital signal processing.
- Division algorithms: There are various algorithms used to perform division in computer arithmetic, including the restoring division algorithm, non-restoring division algorithm, and SRT division algorithm.
- Multiplication algorithms: There are also various algorithms used to perform multiplication in computer arithmetic, including the Booth’s algorithm, the array multiplier, and the Wallace tree multiplier.
Overall, computer arithmetic is a complex and important field that underlies many aspects of modern computing. It involves a wide range of concepts and operations, from basic addition and subtraction to advanced algorithms for multiplication and division.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...