Computer Arithmetic | Set – 1
Last Updated :
23 Apr, 2023
Negative Number Representation
Sign magnitude is a very simple representation of negative numbers. In sign magnitude the first bit is dedicated to represent the sign and hence it is called sign bit.
Sign bit ‘1’ represents negative sign.
Sign bit ‘0’ represents positive sign.
In sign magnitude representation of a n – bit number, the first bit will represent sign and rest n-1 bits represent magnitude of number.
For example,
Where 11001 = 25
And 0 for ‘+’
Where 11001 = 25
And 1 for ‘-‘.
Range of number represented by sign magnitude method = -(2n-1-1) to +(2n-1-1) (for n bit number)
But there is one problem in sign magnitude and that is we have two representations of 0
+0 = 000000
– 0 = 100000
To represent a negative number in this form, first we need to take the 1’s complement of the number represented in simple positive binary form and then add 1 to it.
For example:
(-8)10 = (1000)2
1’s complement of 1000 = 0111
Adding 1 to it, 0111 + 1 = 1000
So, (-8)10 = (1000)2
Please don’t get confused with (8)10 =1000 and (-8)10=1000 as with 4 bits, we can’t represent a positive number more than 7. So, 1000 is representing -8 only.
Range of number represented by 2’s complement = (-2n-1 to 2n-1 – 1)
Floating point representation of numbers
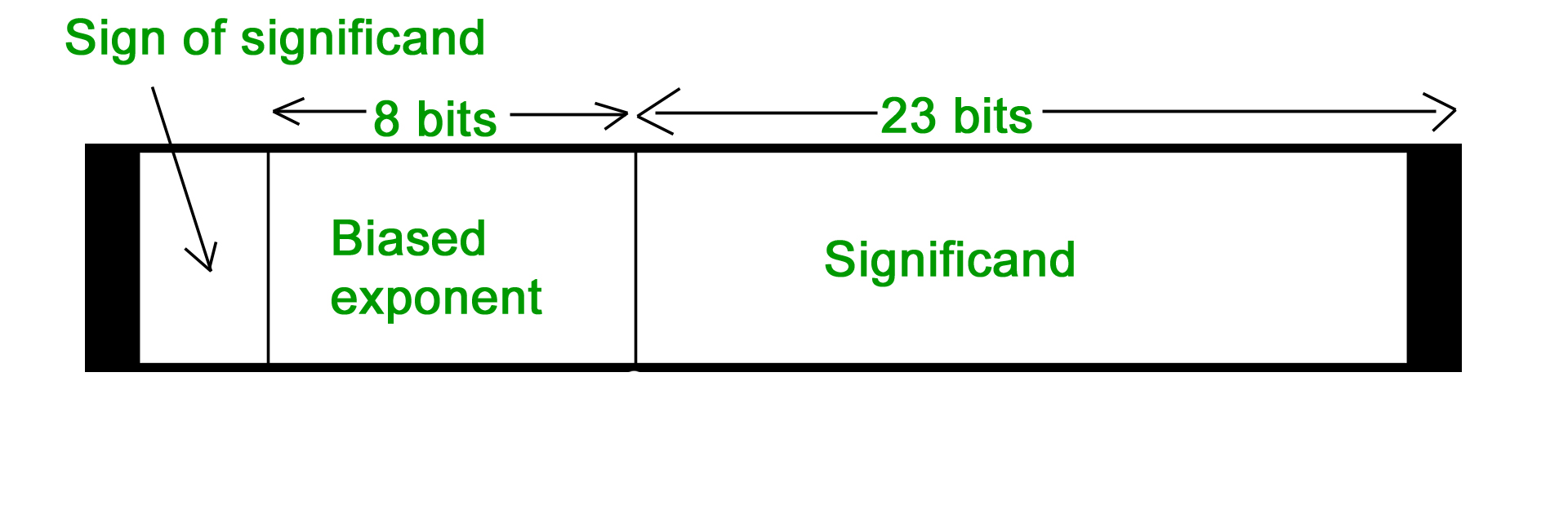
- 32-bit representation floating point numbers IEEE standard
 Normalization
Normalization
- Floating point numbers are usually normalized
- Exponent is adjusted so that leading bit (MSB) of mantissa is 1
- Since it is always 1 there is no need to store it
- Scientific notation where numbers are normalized to give a single digit before the decimal point like in decimal system e.g. 3.123 x 103
For example, we represent 3.625 in 32 bit format. Changing 3 in binary=11 Changing .625 in binary
.625 X 2 1
.25 X 2 0
.5 X 2 1
Writing in binary exponent form
3.625=11.101 X 20
On normalizing
11.101 X 20=1.1101 X 21
On biasing exponent = 127 + 1 = 128
(128)10=(10000000) 2
For getting significand Digits after decimal = 1101 Expanding to 23 bit = 11010000000000000000000 Setting sign bit As it is a positive number, sign bit = 0 Finally we arrange according to representation
Sign bit exponent significand
0 10000000 11010000000000000000000
- 64-bit representation floating point numbers IEEE standard
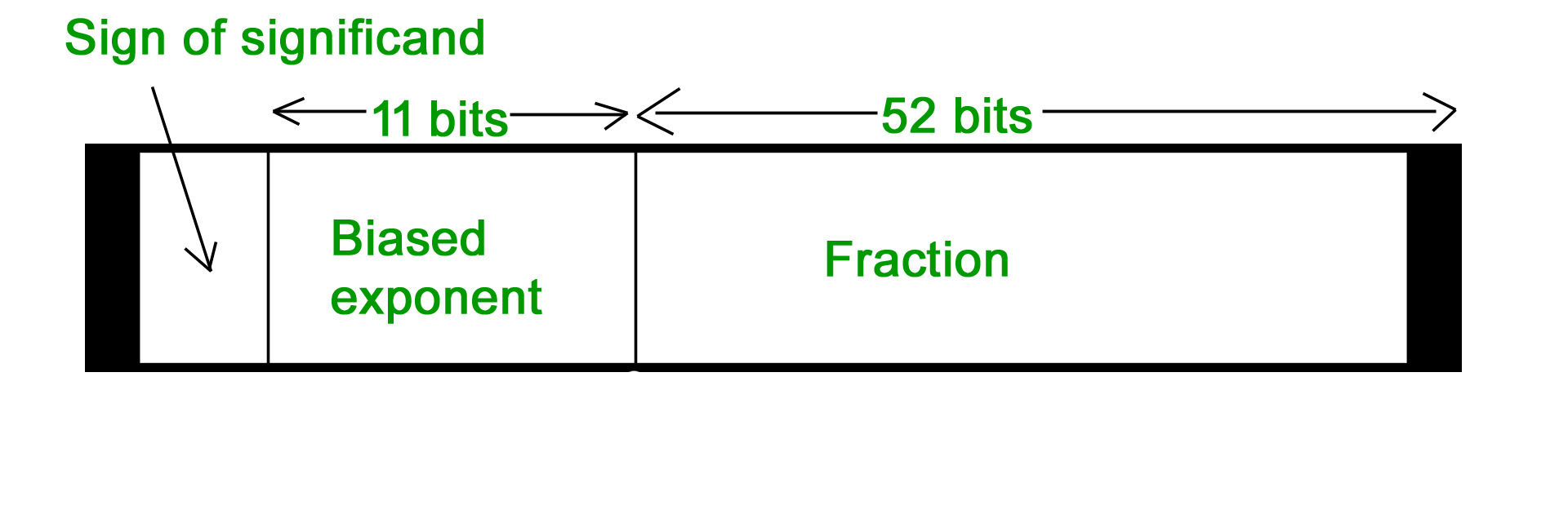 Again we follow the same procedure upto normalization. After that, we add 1023 to bias the exponent. For example, we represent -3.625 in 64 bit format. Changing 3 in binary = 11 Changing .625 in binary
Again we follow the same procedure upto normalization. After that, we add 1023 to bias the exponent. For example, we represent -3.625 in 64 bit format. Changing 3 in binary = 11 Changing .625 in binary
.625 X 2 1
.25 X 2 0
.5 X 2 1
Writing in binary exponent form 3.625 = 11.101 X 20 On normalizing 11.101 X 20 = 1.1101 X 21 On biasing exponent 1023 + 1 = 1024 (1024)10 = (10000000000)2 So 11 bit exponent = 10000000000 52 bit significand = 110100000000 …………. making total 52 bits Setting sign bit = 1 (number is negative) So, final representation 1 10000000000 110100000000 …………. making total 52 bits by adding further 0’s Converting floating point into decimal Let’s convert a FP number into decimal 1 01111100 11000000000000000000000 The decimal value of an IEEE number is given by the formula: (1 -2s) * (1 + f) * 2( e – bias ) where
- s, f and e fields are taken as decimal here.
- (1 -2s) is 1 or -1, depending upon sign bit 0 and 1
- add an implicit 1 to the significand (fraction field f), as in formula
Again, the bias is either 127 or 1023, for single or double precision respectively. First convert each individual field to decimal.
- The sign bit s is 1
- The e field contains 01111100 = (124)10
- The mantissa is 0.11000 … = (0.75)10
Putting these values in formula (1 – 2) * (1 + 0.75) * 2124 – 127 = ( – 1.75 * 2-3 ) = – 0.21875 This article has been contributed by Anuj Batham.
Computer arithmetic is the branch of computer science that deals with the representation and manipulation of numerical quantities in a computer system. Here are some basic concepts and operations involved in computer arithmetic:
- Number systems: Computers use different number systems to represent numerical quantities, including binary (base 2), decimal (base 10), and hexadecimal (base 16) systems. In binary system, each digit can only be either 0 or 1, while in decimal system, each digit can be any of the 10 digits from 0 to 9.
- Arithmetic operations: The basic arithmetic operations used in computer arithmetic are addition, subtraction, multiplication, and division. These operations are usually performed using arithmetic circuits within the CPU.
- Overflow: In computer arithmetic, overflow occurs when the result of an arithmetic operation is too large to be represented in the available number of bits. This can result in incorrect or unexpected results.
- Floating-point arithmetic: Floating-point arithmetic is used to represent and perform operations on non-integer numbers. It involves representing a number as a combination of a mantissa (or significand) and an exponent.
- Round-off errors: Round-off errors occur in floating-point arithmetic due to the limited precision of the number representation. This can result in small inaccuracies in the computed results.
- Bitwise operations: Bitwise operations are used to manipulate individual bits in a number. The basic bitwise operations include AND, OR, XOR, and NOT.
- Two’s complement representation: Two’s complement representation is a method of representing negative numbers in binary. In this representation, the most significant bit is used as a sign bit, with 0 indicating a positive number and 1 indicating a negative number.
Overall, computer arithmetic is a fundamental aspect of computer science and is used in a wide range of applications, including scientific computing, financial analysis, and digital signal processing.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...