Compute nCr%p using Lucas Theorem
Last Updated :
28 Nov, 2022
Given three numbers n, r and p, compute the value of nCr mod p.
Examples:
Input: n = 10, r = 2, p = 13
Output: 6
Explanation: 10C2 is 45 and 45 % 13 is 6.
Input: n = 1000, r = 900, p = 13
Output: 8
We strongly recommend referring below post as a prerequisite of this.
Compute nCr % p | Set 1 (Introduction and Dynamic Programming Solution)
We have introduced overflow problem and discussed Dynamic Programming based solution in above set 1. The time complexity of the DP-based solution is O(n*r) and it required O(n) space. The time taken and extra space become very high for large values of n, especially values close to 109.
In this post, Lucas Theorem-based solution is discussed. The time complexity of this solution is O(p2 * Logp n) and it requires only O(p) space.
Lucas Theorem:
For non-negative integers n and r and a prime p, the following congruence relation holds:
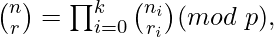
where
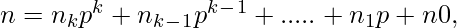
and
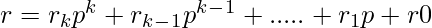
Using Lucas Theorem for nCr % p:
Lucas theorem basically suggests that the value of nCr can be computed by multiplying results of niCri where ni and ri are individual same-positioned digits in base p representations of n and r respectively.
The idea is to one by one compute niCri for individual digits ni and ri in base p. We can compute these values DP based solution discussed in previous post. Since these digits are in base p, we would never need more than O(p) space, and time complexity of these individual computations would be bounded by O(p2).
Below is the implementation of the above idea
C++14
#include<bits/stdc++.h>
using namespace std;
int nCrModpDP(int n, int r, int p)
{
int C[r+1];
memset(C, 0, sizeof(C));
C[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = min(i, r); j > 0; j--)
C[j] = (C[j] + C[j-1])%p;
}
return C[r];
}
int nCrModpLucas(int n, int r, int p)
{
if (r==0)
return 1;
int ni = n%p, ri = r%p;
return (nCrModpLucas(n/p, r/p, p) *
nCrModpDP(ni, ri, p)) % p;
}
int main()
{
int n = 1000, r = 900, p = 13;
cout << "Value of nCr % p is " << nCrModpLucas(n, r, p);
return 0;
}
|
Java
class GFG{
static int nCrModpDP(int n, int r, int p)
{
int[] C=new int[r+1];
C[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = Math.min(i, r); j > 0; j--)
C[j] = (C[j] + C[j-1])%p;
}
return C[r];
}
static int nCrModpLucas(int n, int r, int p)
{
if (r==0)
return 1;
int ni = n%p;
int ri = r%p;
return (nCrModpLucas(n/p, r/p, p) *
nCrModpDP(ni, ri, p)) % p;
}
public static void main(String[] args)
{
int n = 1000, r = 900, p = 13;
System.out.println("Value of nCr % p is "+nCrModpLucas(n, r, p));
}
}
|
Python3
def nCrModpDP(n, r, p):
C = [0] * (n + 1);
C[0] = 1;
for i in range(1, (n + 1)):
j = min(i, r);
while(j > 0):
C[j] = (C[j] + C[j - 1]) % p;
j -= 1;
return C[r];
def nCrModpLucas(n, r, p):
if (r == 0):
return 1;
ni = int(n % p);
ri = int(r % p);
return (nCrModpLucas(int(n / p), int(r / p), p) *
nCrModpDP(ni, ri, p)) % p;
n = 1000;
r = 900;
p = 13;
print("Value of nCr % p is",
nCrModpLucas(n, r, p));
|
C#
using System;
class GFG
{
static int nCrModpDP(int n, int r, int p)
{
int[] C = new int[r + 1];
C[0] = 1;
for (int i = 1; i <= n; i++)
{
for (int j = Math.Min(i, r); j > 0; j--)
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
static int nCrModpLucas(int n, int r, int p)
{
if (r == 0)
return 1;
int ni = n % p;
int ri = r % p;
return (nCrModpLucas(n / p, r / p, p) *
nCrModpDP(ni, ri, p)) % p;
}
public static void Main()
{
int n = 1000, r = 900, p = 13;
Console.Write("Value of nCr % p is " +
nCrModpLucas(n, r, p));
}
}
|
PHP
<?php
function nCrModpDP($n, $r, $p)
{
$C = array_fill(0, $n + 1,
false);
$C[0] = 1;
for ($i = 1; $i <= $n; $i++)
{
for ($j = min($i, $r);
$j > 0; $j--)
$C[$j] = ($C[$j] +
$C[$j - 1]) % $p;
}
return $C[$r];
}
function nCrModpLucas($n, $r, $p)
{
if ($r == 0)
return 1;
$ni = $n % $p;
$ri = $r % $p;
return (nCrModpLucas($n / $p,
$r / $p, $p) *
nCrModpDP($ni, $ri, $p)) % $p;
}
$n = 1000; $r = 900; $p = 13;
echo "Value of nCr % p is " ,
nCrModpLucas($n, $r, $p);
?>
|
Javascript
<script>
function nCrModpDP(n, r, p)
{
C = Array(r+1).fill(0);
C[0] = 1;
for (var i = 1; i <= n; i++)
{
for (var j = Math.min(i, r); j > 0; j--)
C[j] = (C[j] + C[j-1])%p;
}
return C[r];
}
function nCrModpLucas(n, r, p)
{
if (r==0)
return 1;
var ni = n%p, ri = r%p;
return (nCrModpLucas(parseInt(n/p), parseInt(r/p), p) *
nCrModpDP(ni, ri, p)) % p;
}
var n = 1000, r = 900, p = 13;
document.write("Value of nCr % p is " + nCrModpLucas(n, r, p));
</script>
|
OutputValue of nCr % p is 9
Time Complexity: Time complexity of this solution is O(p2 * Logp n). There are O(Logp n) digits in base p representation of n. Each of these digits is smaller than p, therefore, computations for individual digits take O(p2). Note that these computations are done using DP method which takes O(n*r) time.
Auxiliary Space: O(r) as extra space for array C is being used
Alternate Implementation with O(p2 + Logp n) time and O(p2) space:
The idea is to precompute Pascal triangle for size p x p and store it in 2D array. All values needed would now take O(1) time. Therefore overall time complexity becomes O(p2 + Logp n).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...