Comb Sort

Comb Sort is mainly an improvement over Bubble Sort. Bubble sort always compares adjacent values. So all inversions are removed one by one. Comb Sort improves on Bubble Sort by using a gap of the size of more than 1. The gap starts with a large value and shrinks by a factor of 1.3 in every iteration until it reaches the value 1. Thus Comb Sort removes more than one inversion count with one swap and performs better than Bubble Sort.
The shrink factor has been empirically found to be 1.3 (by testing Combsort on over 200,000 random lists) [Source: Wiki]
Although it works better than Bubble Sort on average, worst-case remains O(n²).

Flowchart

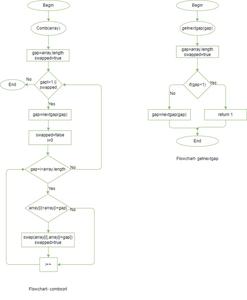
Flowchart

Below is the implementation.

C++

// C++ implementation of Comb Sort
#include<bits/stdc++.h>
using namespace std;

// To find gap between elements
int getNextGap(int gap)
{
    // Shrink gap by Shrink factor
    gap = (gap*10)/13;

    if (gap < 1)
        return 1;
    return gap;
}

// Function to sort a[0..n-1] using Comb Sort
void combSort(int a[], int n)
{
    // Initialize gap
    int gap = n;

    // Initialize swapped as true to make sure that
    // loop runs
    bool swapped = true;

    // Keep running while gap is more than 1 and last
    // iteration caused a swap
    while (gap != 1 || swapped == true)
    {
        // Find next gap
        gap = getNextGap(gap);

        // Initialize swapped as false so that we can
        // check if swap happened or not
        swapped = false;

        // Compare all elements with current gap
        for (int i=0; i<n-gap; i++)
        {
            if (a[i] > a[i+gap])
            {
                swap(a[i], a[i+gap]);
                swapped = true;
            }
        }
    }
}

// Driver program
int main()
{
    int a[] = {8, 4, 1, 56, 3, -44, 23, -6, 28, 0};
    int n = sizeof(a)/sizeof(a[0]);

    combSort(a, n);

    printf("Sorted array: \n");
    for (int i=0; i<n; i++)
        printf("%d ", a[i]);

    return 0;
}

Java

// Java program for implementation of Comb Sort
import java.io.*;
public class CombSort
{
    // To find gap between elements
    int getNextGap(int gap)
    {
        // Shrink gap by Shrink factor
        gap = (gap*10)/13;
        if (gap < 1)
            return 1;
        return gap;
    }

    // Function to sort arr[] using Comb Sort
    void sort(int arr[])
    {
        int n = arr.length;

        // initialize gap
        int gap = n;

        // Initialize swapped as true to make sure that
        // loop runs
        boolean swapped = true;

        // Keep running while gap is more than 1 and last
        // iteration caused a swap
        while (gap != 1 || swapped == true)
        {
            // Find next gap
            gap = getNextGap(gap);

            // Initialize swapped as false so that we can
            // check if swap happened or not
            swapped = false;

            // Compare all elements with current gap
            for (int i=0; i<n-gap; i++)
            {
                if (arr[i] > arr[i+gap])
                {
                    // Swap arr[i] and arr[i+gap]
                    int temp = arr[i];
                    arr[i] = arr[i+gap];
                    arr[i+gap] = temp;

                    // Set swapped
                    swapped = true;
                }
            }
        }
    }

    // Driver method
    public static void main(String args[])
    {
        CombSort ob = new CombSort();
        int arr[] = {8, 4, 1, 56, 3, -44, 23, -6, 28, 0};
        ob.sort(arr);

        System.out.println("sorted array");
        for (int i=0; i<arr.length; ++i)
            System.out.print(arr[i] + " ");

    }
}
/* This code is contributed by Rajat Mishra */

Python3

# Python program for implementation of CombSort

# To find next gap from current
def getNextGap(gap):

    # Shrink gap by Shrink factor
    gap = (gap * 10)//13
    if gap < 1:
        return 1
    return gap

# Function to sort arr[] using Comb Sort
def combSort(arr):
    n = len(arr)

    # Initialize gap
    gap = n

    # Initialize swapped as true to make sure that
    # loop runs
    swapped = True

    # Keep running while gap is more than 1 and last
    # iteration caused a swap
    while gap !=1 or swapped == 1:

        # Find next gap
        gap = getNextGap(gap)

        # Initialize swapped as false so that we can
        # check if swap happened or not
        swapped = False

        # Compare all elements with current gap
        for i in range(0, n-gap):
            if arr[i] > arr[i + gap]:
                arr[i], arr[i + gap]=arr[i + gap], arr[i]
                swapped = True


# Driver code to test above
arr = [8, 4, 1, 56, 3, -44, 23, -6, 28, 0]
combSort(arr)

print ("Sorted array:")
for i in range(len(arr)):
    print (arr[i],end=" ")


# This code is contributed by Mohit Kumra

C#

// C# program for implementation of Comb Sort
using System;

class GFG
{
    // To find gap between elements
    static int getNextGap(int gap)
    {
        // Shrink gap by Shrink factor
        gap = (gap*10)/13;
        if (gap < 1)
            return 1;
        return gap;
    }

    // Function to sort arr[] using Comb Sort
    static void sort(int []arr)
    {
        int n = arr.Length;

        // initialize gap
        int gap = n;

        // Initialize swapped as true to
        // make sure that loop runs
        bool swapped = true;

        // Keep running while gap is more than
        // 1 and last iteration caused a swap
        while (gap != 1 || swapped == true)
        {
            // Find next gap
            gap = getNextGap(gap);

            // Initialize swapped as false so that we can
            // check if swap happened or not
            swapped = false;

            // Compare all elements with current gap
            for (int i=0; i<n-gap; i++)
            {
                if (arr[i] > arr[i+gap])
                {
                    // Swap arr[i] and arr[i+gap]
                    int temp = arr[i];
                    arr[i] = arr[i+gap];
                    arr[i+gap] = temp;

                    // Set swapped
                    swapped = true;
                }
            }
        }
    }

    // Driver method
    public static void Main()
    {
        int []arr = {8, 4, 1, 56, 3, -44, 23, -6, 28, 0};
        sort(arr);

        Console.WriteLine("sorted array");
        for (int i=0; i<arr.Length; ++i)
            Console.Write(arr[i] + " ");

    }
}

// This code is contributed by Sam007

Javascript

<script>
    // Javascript program for implementation of Comb Sort

    // To find gap between elements
    function getNextGap(gap)
    {
        // Shrink gap by Shrink factor
        gap = parseInt((gap*10)/13, 10);
        if (gap < 1)
            return 1;
        return gap;
    }

    // Function to sort arr[] using Comb Sort
    function sort(arr)
    {
        let n = arr.length;

        // initialize gap
        let gap = n;

        // Initialize swapped as true to
        // make sure that loop runs
        let swapped = true;

        // Keep running while gap is more than
        // 1 and last iteration caused a swap
        while (gap != 1 || swapped == true)
        {
            // Find next gap
            gap = getNextGap(gap);

            // Initialize swapped as false so that we can
            // check if swap happened or not
            swapped = false;

            // Compare all elements with current gap
            for (let i=0; i<n-gap; i++)
            {
                if (arr[i] > arr[i+gap])
                {
                    // Swap arr[i] and arr[i+gap]
                    let temp = arr[i];
                    arr[i] = arr[i+gap];
                    arr[i+gap] = temp;

                    // Set swapped
                    swapped = true;
                }
            }
        }
    }

    let arr = [8, 4, 1, 56, 3, -44, 23, -6, 28, 0];
    sort(arr);

    document.write("sorted array" + "</br>");
    for (let i=0; i<arr.length; ++i)
      document.write(arr[i] + " ");

 // This code is contributed by decode2207
</script>

Output

Sorted array: 
-44 -6 0 1 3 4 8 23 28 56 

Illustration:
Let the array elements be 

8, 4, 1, 56, 3, -44, 23, -6, 28, 0

Initially gap value = 10 
After shrinking gap value => 10/1.3 = 7; 

 8 4 1 56 3 -44 23 -6 28 0
-6 4 1 56 3 -44 23  8 28 0
-6 4 0 56 3 -44 23  8 28 1

New gap value => 7/1.3 = 5;  

-44 4 0 56 3 -6 23 8 28 1
-44 4 0 28 3 -6 23 8 56 1
-44 4 0 28 1 -6 23 8 56 3

New gap value => 5/1.3 = 3; 

-44 1  0 28 4 -6 23 8 56 3
-44 1 -6 28 4  0 23 8 56 3
-44 1 -6 23 4  0 28 8 56 3
-44 1 -6 23 4  0  3 8 56 28

New gap value => 3/1.3 = 2;  

-44 1 -6 0 4 23 3 8 56 28
-44 1 -6 0 3 23 4 8 56 28
-44 1 -6 0 3 8 4 23 56 28

New gap value => 2/1.3 = 1;  

-44 -6 1 0 3 8 4 23 56 28
-44 -6 0 1 3 8 4 23 56 28
-44 -6 0 1 3 4 8 23 56 28
-44 -6 0 1 3 4 8 23 28 56 

no more swaps required (Array sorted)

Time Complexity: Average case time complexity of the algorithm is Ω(N²/2^p), where p is the number of increments. The worst-case complexity of this algorithm is O(n²) and the Best Case complexity is O(nlogn). 
Auxiliary Space : O(1). 

Quiz on Comb Sort

This article is contributed by Rahul Agrawal. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks. 

Snapshots:

Other Sorting Algorithms on GeeksforGeeks/GeeksQuiz
Selection Sort, Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort, Pigeonhole Sort
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.