Check if a given graph is tree or not
Last Updated :
06 Feb, 2023
Write a function that returns true if a given undirected graph is a tree and false otherwise. For example, the following graph is a tree.

But the following graph is not a tree.
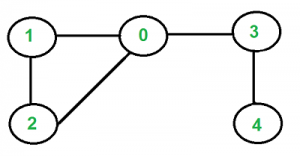
Approach 1:
An undirected graph is a tree if it has the following properties.
- There is no cycle.
- The graph is connected.
For an undirected graph, we can either use BFS or DFS to detect the above two properties.
How to detect cycles in an undirected graph?
We can either use BFS or DFS. For every visited vertex ‘v’, if there is an adjacent ‘u’ such that u is already visited and u is not the parent of v, then there is a cycle in the graph. If we don’t find such an adjacent for any vertex, we say that there is no cycle (See Detect cycle in an undirected graph for more details).
How to check for connectivity?
Since the graph is undirected, we can start BFS or DFS from any vertex and check if all vertices are reachable or not. If all vertices are reachable, then the graph is connected, otherwise not.
Implementation:
C++
#include<iostream>
#include <list>
#include <limits.h>
using namespace std;
class Graph
{
int V;
list<int> *adj;
bool isCyclicUtil(int v, bool visited[], int parent);
public:
Graph(int V);
void addEdge(int v, int w);
bool isTree();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v);
}
bool Graph::isCyclicUtil(int v, bool visited[], int parent)
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
{
if (!visited[*i])
{
if (isCyclicUtil(*i, visited, v))
return true;
}
else if (*i != parent)
return true;
}
return false;
}
bool Graph::isTree()
{
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
if (isCyclicUtil(0, visited, -1))
return false;
for (int u = 0; u < V; u++)
if (!visited[u])
return false;
return true;
}
int main()
{
Graph g1(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.isTree()? cout << "Graph is Tree\n":
cout << "Graph is not Tree\n";
Graph g2(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
g2.isTree()? cout << "Graph is Tree\n":
cout << "Graph is not Tree\n";
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class Graph
{
private int V;
private LinkedList<Integer> adj[];
@SuppressWarnings("unchecked")
Graph(int v)
{
V = v;
adj = new LinkedList[V];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList<Integer>();
}
void addEdge(int v,int w)
{
adj[v].add(w);
adj[w].add(v);
}
boolean isCyclicUtil(int v, boolean visited[], int parent)
{
visited[v] = true;
Integer i;
Iterator<Integer> it = adj[v].iterator();
while (it.hasNext())
{
i = it.next();
if (!visited[i])
{
if (isCyclicUtil(i, visited, v))
return true;
}
else if (i != parent)
return true;
}
return false;
}
boolean isTree()
{
boolean visited[] = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
if (isCyclicUtil(0, visited, -1))
return false;
for (int u = 0; u < V; u++)
if (!visited[u])
return false;
return true;
}
public static void main(String args[])
{
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
if (g1.isTree())
System.out.println("Graph is Tree");
else
System.out.println("Graph is not Tree");
Graph g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
if (g2.isTree())
System.out.println("Graph is Tree");
else
System.out.println("Graph is not Tree");
}
}
|
Python3
from collections import defaultdict
class Graph():
def __init__(self, V):
self.V = V
self.graph = defaultdict(list)
def addEdge(self, v, w):
self.graph[v].append(w)
self.graph[w].append(v)
def isCyclicUtil(self, v, visited, parent):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
if self.isCyclicUtil(i, visited, v) == True:
return True
elif i != parent:
return True
return False
def isTree(self):
visited = [False] * self.V
if self.isCyclicUtil(0, visited, -1) == True:
return False
for i in range(self.V):
if visited[i] == False:
return False
return True
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(0, 3)
g1.addEdge(3, 4)
print ("Graph is a Tree" if g1.isTree() == True \
else "Graph is a not a Tree")
g2 = Graph(5)
g2.addEdge(1, 0)
g2.addEdge(0, 2)
g2.addEdge(2, 1)
g2.addEdge(0, 3)
g2.addEdge(3, 4)
print ("Graph is a Tree" if g2.isTree() == True \
else "Graph is a not a Tree")
|
C#
using System;
using System.Collections.Generic;
class Graph
{
private int V;
private List<int> []adj;
Graph(int v)
{
V = v;
adj = new List<int>[v];
for (int i = 0; i < v; ++i)
adj[i] = new List<int>();
}
void addEdge(int v, int w)
{
adj[v].Add(w);
adj[w].Add(v);
}
Boolean isCyclicUtil(int v, Boolean []visited,
int parent)
{
visited[v] = true;
int i;
foreach(int it in adj[v])
{
i = it;
if (!visited[i])
{
if (isCyclicUtil(i, visited, v))
return true;
}
else if (i != parent)
return true;
}
return false;
}
Boolean isTree()
{
Boolean []visited = new Boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
if (isCyclicUtil(0, visited, -1))
return false;
for (int u = 0; u < V; u++)
if (!visited[u])
return false;
return true;
}
public static void Main(String []args)
{
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
if (g1.isTree())
Console.WriteLine("Graph is Tree");
else
Console.WriteLine("Graph is not Tree");
Graph g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
if (g2.isTree())
Console.WriteLine("Graph is Tree");
else
Console.WriteLine("Graph is not Tree");
}
}
|
Javascript
<script>
var V = 0;
var adj;
function initialize(v)
{
V = v;
adj = Array.from(Array(v), ()=>Array());
}
function addEdge(v, w)
{
adj[v].push(w);
adj[w].push(v);
}
function isCyclicUtil(v, visited, parent)
{
visited[v] = true;
var i;
for(var it of adj[v])
{
i = it;
if (!visited[i])
{
if (isCyclicUtil(i, visited, v))
return true;
}
else if (i != parent)
return true;
}
return false;
}
function isTree()
{
var visited = Array(V).fill(false);
if (isCyclicUtil(0, visited, -1))
return false;
for (var u = 0; u < V; u++)
if (!visited[u])
return false;
return true;
}
initialize(5)
addEdge(1, 0);
addEdge(0, 2);
addEdge(0, 3);
addEdge(3, 4);
if (isTree())
document.write("Graph is Tree<br>");
else
document.write("Graph is not Tree<br>");
initialize(5)
addEdge(1, 0);
addEdge(0, 2);
addEdge(2, 1);
addEdge(0, 3);
addEdge(3, 4);
if (isTree())
document.write("Graph is Tree<br>");
else
document.write("Graph is not Tree<br>");
</script>
|
Output
Graph is Tree
Graph is not Tree
Time Complexity: O(V + E)
Auxiliary Space: O(V) as we are using the visited array.
Approach 2:
However if we observe carefully the definition of tree and its structure we will deduce that if a graph is connected and has n – 1 edges exactly then the graph is a tree.
Proof:
Since we have assumed our graph of n nodes to be connected, it must have at least n – 1 edges inside it. Now if we try to add one more edge than the n – 1 edges already the graph will end up forming a cycle and thus will not satisfy the definition of tree. Therefore, it is necessary for a connected graph to have exactly n – 1 edges to avoid forming cycle.
C++
#include<iostream>
#include <list>
#include <limits.h>
using namespace std;
class Graph
{
int V;
int E;
list<int> *adj;
void dfsTraversal(int v, bool visited[], int parent);
public:
Graph(int V);
void addEdge(int v, int w);
bool isConnected();
bool isTree();
};
Graph::Graph(int V)
{
E = 0;
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
E++;
adj[v].push_back(w);
adj[w].push_back(v);
}
void Graph::dfsTraversal(int v, bool visited[], int parent)
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
{
if (!visited[*i])
{
dfsTraversal(*i, visited, v);
}
}
}
bool Graph::isConnected()
{
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
dfsTraversal(0, visited, -1);
for (int u = 0; u < V; u++)
if (!visited[u])
return false;
return true;
}
bool Graph::isTree()
{
return isConnected() and E == V - 1;
}
int main()
{
Graph g1(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.isTree()? cout << "Graph is Tree\n":
cout << "Graph is not Tree\n";
Graph g2(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
g2.isTree()? cout << "Graph is Tree\n":
cout << "Graph is not Tree\n";
return 0;
}
|
Java
import java.util.*;
class Graph {
public static int V;
public static int E;
public static ArrayList<ArrayList<Integer> >
adj;
public Graph(int V)
{
E = 0;
this.V = V;
adj = new ArrayList<ArrayList<Integer> >(V);
for (int i = 0; i < V; i++)
adj.add(new ArrayList<Integer>());
}
static void dfsTraversal(int v, boolean[] visited,
int parent)
{
visited[v] = true;
for (int i : adj.get(v)) {
if (!visited[i]) {
dfsTraversal(i, visited, v);
}
}
}
public static void addEdge(int v, int w)
{
E++;
adj.get(w).add(v);
adj.get(v).add(w);
}
public static boolean isConnected()
{
boolean[] visited = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
dfsTraversal(0, visited, -1);
for (int u = 0; u < V; u++)
if (!visited[u])
return false;
return true;
}
public static boolean isTree()
{
return isConnected() && E == V - 1;
}
}
class Main {
public static void main(String[] args)
{
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
if (g1.isTree())
System.out.println("Graph is Tree");
else
System.out.println("Graph is not Tree");
Graph g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
if (g2.isTree())
System.out.println("Graph is Tree");
else
System.out.println("Graph is not Tree");
}
}
|
Python3
class Graph:
def __init__(self, V):
self.V = V
self.E = 0
self.adj = [[] for i in range(V)]
def addEdge(self, v, w):
self.E += 1
self.adj[v].append(w)
self.adj[w].append(v)
def dfsTraversal(self, v, visited, parent):
visited[v] = True
for i in self.adj[v]:
if not visited[i]:
self.dfsTraversal(i, visited, v)
def isConnected(self):
visited = [False] * self.V
self.dfsTraversal(0, visited, -1)
for u in range(self.V):
if not visited[u]:
return False
return True
def isTree(self):
return self.isConnected() and self.E == self.V - 1
if __name__ == '__main__':
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(0, 3)
g1.addEdge(3, 4)
print("Graph is Tree" if g1.isTree() == True else "Graph is not Tree")
g2 = Graph(5)
g2.addEdge(1, 0)
g2.addEdge(0, 2)
g2.addEdge(2, 1)
g2.addEdge(0, 3)
g2.addEdge(3, 4)
print("Graph is Tree" if g2.isTree() == True else "Graph is not Tree")
|
C#
using System;
using System.Collections.Generic;
class Graph {
public int V;
public int E;
public static List<List<int> >
adj;
public Graph(int V)
{
E = 0;
this.V = V;
adj = new List<List<int> >(V);
for (int i = 0; i < V; i++)
adj.Add(new List<int>());
}
static void dfsTraversal(int v, bool[] visited,
int parent)
{
visited[v] = true;
foreach(var i in adj[v])
{
if (!visited[i]) {
dfsTraversal(i, visited, v);
}
}
}
public void addEdge(int v, int w)
{
E++;
adj[w].Add(v);
adj[v].Add(w);
}
public bool isConnected()
{
bool[] visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
dfsTraversal(0, visited, -1);
for (int u = 0; u < V; u++)
if (!visited[u])
return false;
return true;
}
public bool isTree()
{
return isConnected() && E == V - 1;
}
}
class Program {
public static void Main(string[] args)
{
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
if (g1.isTree())
Console.WriteLine("Graph is Tree");
else
Console.WriteLine("Graph is not Tree");
Graph g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
if (g2.isTree())
Console.WriteLine("Graph is Tree");
else
Console.WriteLine("Graph is not Tree");
}
}
|
Javascript
class Graph {
constructor(V) {
this.V = V;
this.E = 0;
this.adj = [];
for (var i = 0; i < V; i++) {
this.adj[i] = [];
}
}
addEdge(v, w) {
this.E++;
this.adj[v].push(w);
this.adj[w].push(v);
}
dfsTraversal(v, visited, parent) {
visited[v] = true;
for (var i of this.adj[v]) {
if (!visited[i]) {
this.dfsTraversal(i, visited, v);
}
}
}
isConnected() {
var visited = new Array(this.V);
for (var i = 0; i < this.V; i++) {
visited[i] = false;
}
this.dfsTraversal(0, visited, -1);
for (var u = 0; u < this.V; u++) {
if (!visited[u]) {
return false;
}
}
return true;
}
isTree() {
return this.isConnected() && this.E == this.V - 1;
}
}
let g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.isTree() ? console.log("Graph is Tree") : console.log("Graph is not Tree");
let g2 = new Graph(5);
g2.addEdge(1, 0);
g2.addEdge(0, 2);
g2.addEdge(2, 1);
g2.addEdge(0, 3);
g2.addEdge(3, 4);
g2.isTree() ? console.log("Graph is Tree") : console.log("Graph is not Tree");
|
Output
Graph is Tree
Graph is not Tree
Time Complexity: O(V + E) For performing the DFS traversal
Auxiliary Space: O(V) For storing the visited array
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...