Bridges in a graph

Given an undirected Graph, The task is to find the Bridges in this Graph. 

An edge in an undirected connected graph is a bridge if removing it disconnects the graph. For a disconnected undirected graph, the definition is similar, a bridge is an edge removal that increases the number of disconnected components. 

Like Articulation Points, bridges represent vulnerabilities in a connected network and are useful for designing reliable networks.

Examples:

Input: 

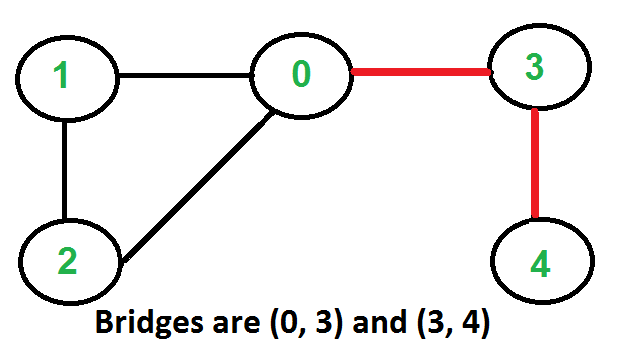
Output: (0, 3) and (3, 4)

Input:

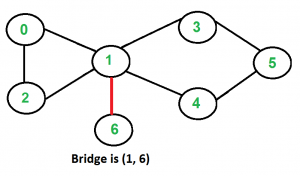
Output: (1, 6)

Input:

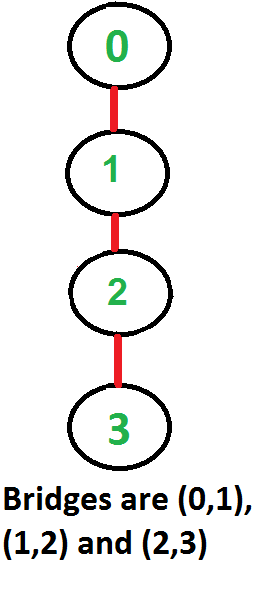
Output: (0, 1), (1, 2), and (2, 3)

Naive Approach: Below is the idea to solve the problem:

One by one remove all edges and see if the removal of an edge causes a disconnected graph. 

Follow the below steps to Implement the idea:

• For every edge (u, v), do the following:
  • Remove (u, v) from the graph 
  • See if the graph remains connected (either uses BFS or DFS) 
  • Add (u, v) back to the graph.

Time Complexity: O(E*(V+E)) for a graph represented by an adjacency list.
Auxiliary Space: O(V+E)

Find Bridges in a graph using Tarjan’s Algorithm.

Before heading towards the approach understand which edge is termed as bridge. Suppose there exists a edge from u -> v, now after removal of this edge if v can’t be reached by any other edges then u -> v edge is bridge. Our approach is based on this intuition, so take time and grasp it.

ALGORITHM: –

To implement this algorithm, we need the following data structures –

• visited[ ] = to keep track of the visited vertices to implement DFS
• disc[ ] = to keep track when for the first time that particular vertex is reached
• low[ ] = to keep track of the lowest possible time by which we can reach that vertex ‘other than parent’ so that if edge from parent is removed can the particular node can be reached other than parent.

We will traverse the graph using DFS traversal but with slight modifications i.e. while traversing we will keep track of the parent node by which the particular node is reached because we will update the low[node] = min(low[all it’s adjacent node except parent]) hence we need to keep track of the parent.

While traversing adjacent nodes let ‘v’ of a particular node let ‘u’ 3 cases arise –

1. v is parent of u then, 

• skip that iteration.

2. v is visited then,

• update the low of v i.e. low[u] = min( low[u] , disc[v]) this arises when a node can be visited by more than one node, but low is to keep track of the lowest possible time so we will update it.

3. v is not visited then,

• call the DFS to traverse ahead
• now update the low[u] = min( low[u], low[v] ) as we know v can’t be parent cause we have handled that case first.
• now check if ( low[v] > disc[u] ) i.e. the lowest possible to time to reach ‘v’ is greater than ‘u’ this means we can’t reach ‘v’ without ‘u’ so the edge   u -> v is a bridge.

Below is the implementation of the above approach:

C++

// A C++ program to find bridges in a given undirected graph
#include<bits/stdc++.h>
using namespace std;

// A class that represents an undirected graph
class Graph
{
    int V;    // No. of vertices
    list<int> *adj;    // A dynamic array of adjacency lists
    void bridgeUtil(int u, vector<bool>& visited, vector<int>& disc,
                                  vector<int>& low, int parent);
public:
    Graph(int V);   // Constructor
    void addEdge(int v, int w);   // to add an edge to graph
    void bridge();    // prints all bridges
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w);
    adj[w].push_back(v);  // Note: the graph is undirected
}

// A recursive function that finds and prints bridges using
// DFS traversal
// u --> The vertex to be visited next
// visited[] --> keeps track of visited vertices
// disc[] --> Stores discovery times of visited vertices
// parent[] --> Stores parent vertices in DFS tree
void Graph::bridgeUtil(int u, vector<bool>& visited, vector<int>& disc,
                                  vector<int>& low, int parent)
{
    // A static variable is used for simplicity, we can
    // avoid use of static variable by passing a pointer.
    static int time = 0;

    // Mark the current node as visited
    visited[u] = true;

    // Initialize discovery time and low value
    disc[u] = low[u] = ++time;

    // Go through all vertices adjacent to this
    list<int>::iterator i;
    for (i = adj[u].begin(); i != adj[u].end(); ++i)
    {
        int v = *i;  // v is current adjacent of u

          // 1. If v is parent
          if(v==parent)
            continue;

          //2. If v is visited
          if(visited[v]){
          low[u]  = min(low[u], disc[v]);
        }

          //3. If v is not visited
          else{
          parent = u;
          bridgeUtil(v, visited, disc, low, parent);

          // update the low of u as it's quite possible
          // a connection exists from v's descendants to u
          low[u]  = min(low[u], low[v]);

          // if the lowest possible time to reach vertex v
          // is greater than discovery time of u it means
          // that v can be only be reached by vertex above v
          // so if that edge is removed v can't be reached so it's a bridge
          if (low[v] > disc[u])
              cout << u <<" " << v << endl;

        }
    }
}

// DFS based function to find all bridges. It uses recursive
// function bridgeUtil()
void Graph::bridge()
{
    // Mark all the vertices as not visited disc and low as -1
    vector<bool> visited (V,false);
    vector<int> disc (V,-1);
      vector<int> low (V,-1);

      // Initially there is no parent so let it be -1
      int parent = -1;

    // Call the recursive helper function to find Bridges
    // in DFS tree rooted with vertex 'i'
    for (int i = 0; i < V; i++)
        if (visited[i] == false)
            bridgeUtil(i, visited, disc, low, parent);
}

// Driver program to test above function
int main()
{
    // Create graphs given in above diagrams
    cout << "\nBridges in first graph \n";
    Graph g1(5);
    g1.addEdge(1, 0);
    g1.addEdge(0, 2);
    g1.addEdge(2, 1);
    g1.addEdge(0, 3);
    g1.addEdge(3, 4);
    g1.bridge();

    cout << "\nBridges in second graph \n";
    Graph g2(4);
    g2.addEdge(0, 1);
    g2.addEdge(1, 2);
    g2.addEdge(2, 3);
    g2.bridge();

    cout << "\nBridges in third graph \n";
    Graph g3(7);
    g3.addEdge(0, 1);
    g3.addEdge(1, 2);
    g3.addEdge(2, 0);
    g3.addEdge(1, 3);
    g3.addEdge(1, 4);
    g3.addEdge(1, 6);
    g3.addEdge(3, 5);
    g3.addEdge(4, 5);
    g3.bridge();

    return 0;
}

Java

// A Java program to find bridges in a given undirected graph
import java.io.*;
import java.util.*;
import java.util.LinkedList;

// This class represents a undirected graph using adjacency list
// representation
class Graph
{
    private int V;   // No. of vertices

    // Array  of lists for Adjacency List Representation
    private LinkedList<Integer> adj[];
    int time = 0;
    static final int NIL = -1;

    // Constructor
    @SuppressWarnings("unchecked")Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int i=0; i<v; ++i)
            adj[i] = new LinkedList();
    }

    // Function to add an edge into the graph
    void addEdge(int v, int w)
    {
        adj[v].add(w);  // Add w to v's list.
        adj[w].add(v);    //Add v to w's list
    }

    // A recursive function that finds and prints bridges
    // using DFS traversal
    // u --> The vertex to be visited next
    // visited[] --> keeps track of visited vertices
    // disc[] --> Stores discovery times of visited vertices
    // parent[] --> Stores parent vertices in DFS tree
    void bridgeUtil(int u, boolean visited[], int disc[],
                    int low[], int parent[])
    {

        // Mark the current node as visited
        visited[u] = true;

        // Initialize discovery time and low value
        disc[u] = low[u] = ++time;

        // Go through all vertices adjacent to this
        Iterator<Integer> i = adj[u].iterator();
        while (i.hasNext())
        {
            int v = i.next();  // v is current adjacent of u

            // If v is not visited yet, then make it a child
            // of u in DFS tree and recur for it.
            // If v is not visited yet, then recur for it
            if (!visited[v])
            {
                parent[v] = u;
                bridgeUtil(v, visited, disc, low, parent);

                // Check if the subtree rooted with v has a
                // connection to one of the ancestors of u
                low[u]  = Math.min(low[u], low[v]);

                // If the lowest vertex reachable from subtree
                // under v is below u in DFS tree, then u-v is
                // a bridge
                if (low[v] > disc[u])
                    System.out.println(u+" "+v);
            }

            // Update low value of u for parent function calls.
            else if (v != parent[u])
                low[u]  = Math.min(low[u], disc[v]);
        }
    }


    // DFS based function to find all bridges. It uses recursive
    // function bridgeUtil()
    void bridge()
    {
        // Mark all the vertices as not visited
        boolean visited[] = new boolean[V];
        int disc[] = new int[V];
        int low[] = new int[V];
        int parent[] = new int[V];


        // Initialize parent and visited, and ap(articulation point)
        // arrays
        for (int i = 0; i < V; i++)
        {
            parent[i] = NIL;
            visited[i] = false;
        }

        // Call the recursive helper function to find Bridges
        // in DFS tree rooted with vertex 'i'
        for (int i = 0; i < V; i++)
            if (visited[i] == false)
                bridgeUtil(i, visited, disc, low, parent);
    }

    public static void main(String args[])
    {
        // Create graphs given in above diagrams
        System.out.println("Bridges in first graph ");
        Graph g1 = new Graph(5);
        g1.addEdge(1, 0);
        g1.addEdge(0, 2);
        g1.addEdge(2, 1);
        g1.addEdge(0, 3);
        g1.addEdge(3, 4);
        g1.bridge();
        System.out.println();

        System.out.println("Bridges in Second graph");
        Graph g2 = new Graph(4);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        g2.addEdge(2, 3);
        g2.bridge();
        System.out.println();

        System.out.println("Bridges in Third graph ");
        Graph g3 = new Graph(7);
        g3.addEdge(0, 1);
        g3.addEdge(1, 2);
        g3.addEdge(2, 0);
        g3.addEdge(1, 3);
        g3.addEdge(1, 4);
        g3.addEdge(1, 6);
        g3.addEdge(3, 5);
        g3.addEdge(4, 5);
        g3.bridge();
    }
}
// This code is contributed by Aakash Hasija

Python3

# Python program to find bridges in a given undirected graph
#Complexity : O(V+E)

from collections import defaultdict

#This class represents an undirected graph using adjacency list representation
class Graph:

    def __init__(self,vertices):
        self.V= vertices #No. of vertices
        self.graph = defaultdict(list) # default dictionary to store graph
        self.Time = 0

    # function to add an edge to graph
    def addEdge(self,u,v):
        self.graph[u].append(v)
        self.graph[v].append(u)

    '''A recursive function that finds and prints bridges
    using DFS traversal
    u --> The vertex to be visited next
    visited[] --> keeps track of visited vertices
    disc[] --> Stores discovery times of visited vertices
    parent[] --> Stores parent vertices in DFS tree'''
    def bridgeUtil(self,u, visited, parent, low, disc):

        # Mark the current node as visited and print it
        visited[u]= True

        # Initialize discovery time and low value
        disc[u] = self.Time
        low[u] = self.Time
        self.Time += 1

        #Recur for all the vertices adjacent to this vertex
        for v in self.graph[u]:
            # If v is not visited yet, then make it a child of u
            # in DFS tree and recur for it
            if visited[v] == False :
                parent[v] = u
                self.bridgeUtil(v, visited, parent, low, disc)

                # Check if the subtree rooted with v has a connection to
                # one of the ancestors of u
                low[u] = min(low[u], low[v])


                ''' If the lowest vertex reachable from subtree
                under v is below u in DFS tree, then u-v is
                a bridge'''
                if low[v] > disc[u]:
                    print ("%d %d" %(u,v))


            elif v != parent[u]: # Update low value of u for parent function calls.
                low[u] = min(low[u], disc[v])


    # DFS based function to find all bridges. It uses recursive
    # function bridgeUtil()
    def bridge(self):

        # Mark all the vertices as not visited and Initialize parent and visited,
        # and ap(articulation point) arrays
        visited = [False] * (self.V)
        disc = [float("Inf")] * (self.V)
        low = [float("Inf")] * (self.V)
        parent = [-1] * (self.V)

        # Call the recursive helper function to find bridges
        # in DFS tree rooted with vertex 'i'
        for i in range(self.V):
            if visited[i] == False:
                self.bridgeUtil(i, visited, parent, low, disc)


# Create a graph given in the above diagram
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(2, 1)
g1.addEdge(0, 3)
g1.addEdge(3, 4)


print ("Bridges in first graph ")
g1.bridge()

g2 = Graph(4)
g2.addEdge(0, 1)
g2.addEdge(1, 2)
g2.addEdge(2, 3)
print ("\nBridges in second graph ")
g2.bridge()


g3 = Graph (7)
g3.addEdge(0, 1)
g3.addEdge(1, 2)
g3.addEdge(2, 0)
g3.addEdge(1, 3)
g3.addEdge(1, 4)
g3.addEdge(1, 6)
g3.addEdge(3, 5)
g3.addEdge(4, 5)
print ("\nBridges in third graph ")
g3.bridge()


#This code is contributed by Neelam Yadav

C#

// A C# program to find bridges
// in a given undirected graph
using System;
using System.Collections.Generic;

// This class represents a undirected graph
// using adjacency list representation
public class Graph
{
    private int V; // No. of vertices

    // Array of lists for Adjacency List Representation
    private List<int> []adj;
    int time = 0;
    static readonly int NIL = -1;

    // Constructor
    Graph(int v)
    {
        V = v;
        adj = new List<int>[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new List<int>();
    }

    // Function to add an edge into the graph
    void addEdge(int v, int w)
    {
        adj[v].Add(w); // Add w to v's list.
        adj[w].Add(v); //Add v to w's list
    }

    // A recursive function that finds and prints bridges
    // using DFS traversal
    // u --> The vertex to be visited next
    // visited[] --> keeps track of visited vertices
    // disc[] --> Stores discovery times of visited vertices
    // parent[] --> Stores parent vertices in DFS tree
    void bridgeUtil(int u, bool []visited, int []disc,
                    int []low, int []parent)
    {

        // Mark the current node as visited
        visited[u] = true;

        // Initialize discovery time and low value
        disc[u] = low[u] = ++time;

        // Go through all vertices adjacent to this
        foreach(int i in adj[u])
        {
            int v = i; // v is current adjacent of u

            // If v is not visited yet, then make it a child
            // of u in DFS tree and recur for it.
            // If v is not visited yet, then recur for it
            if (!visited[v])
            {
                parent[v] = u;
                bridgeUtil(v, visited, disc, low, parent);

                // Check if the subtree rooted with v has a
                // connection to one of the ancestors of u
                low[u] = Math.Min(low[u], low[v]);

                // If the lowest vertex reachable from subtree
                // under v is below u in DFS tree, then u-v is
                // a bridge
                if (low[v] > disc[u])
                    Console.WriteLine(u + " " + v);
            }

            // Update low value of u for parent function calls.
            else if (v != parent[u])
                low[u] = Math.Min(low[u], disc[v]);
        }
    }


    // DFS based function to find all bridges. It uses recursive
    // function bridgeUtil()
    void bridge()
    {
        // Mark all the vertices as not visited
        bool []visited = new bool[V];
        int []disc = new int[V];
        int []low = new int[V];
        int []parent = new int[V];


        // Initialize parent and visited,
        // and ap(articulation point) arrays
        for (int i = 0; i < V; i++)
        {
            parent[i] = NIL;
            visited[i] = false;
        }

        // Call the recursive helper function to find Bridges
        // in DFS tree rooted with vertex 'i'
        for (int i = 0; i < V; i++)
            if (visited[i] == false)
                bridgeUtil(i, visited, disc, low, parent);
    }

    // Driver code
    public static void Main(String []args)
    {
        // Create graphs given in above diagrams
        Console.WriteLine("Bridges in first graph ");
        Graph g1 = new Graph(5);
        g1.addEdge(1, 0);
        g1.addEdge(0, 2);
        g1.addEdge(2, 1);
        g1.addEdge(0, 3);
        g1.addEdge(3, 4);
        g1.bridge();
        Console.WriteLine();

        Console.WriteLine("Bridges in Second graph");
        Graph g2 = new Graph(4);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        g2.addEdge(2, 3);
        g2.bridge();
        Console.WriteLine();

        Console.WriteLine("Bridges in Third graph ");
        Graph g3 = new Graph(7);
        g3.addEdge(0, 1);
        g3.addEdge(1, 2);
        g3.addEdge(2, 0);
        g3.addEdge(1, 3);
        g3.addEdge(1, 4);
        g3.addEdge(1, 6);
        g3.addEdge(3, 5);
        g3.addEdge(4, 5);
        g3.bridge();
    }
}

// This code is contributed by Rajput-Ji

Javascript

<script>
// A Javascript program to find bridges in a given undirected graph

// This class represents a directed graph using adjacency
// list representation
class Graph
{
    // Constructor
    constructor(v)
    {
        this.V = v;
        this.adj = new Array(v);

        this.NIL = -1;
        this.time = 0;
        for (let i=0; i<v; ++i)
            this.adj[i] = [];
    }

    //Function to add an edge into the graph
    addEdge(v,w)
    {
        this.adj[v].push(w);  //Note that the graph is undirected.
        this.adj[w].push(v);
    }

    // A recursive function that finds and prints bridges
    // using DFS traversal
    // u --> The vertex to be visited next
    // visited[] --> keeps track of visited vertices
    // disc[] --> Stores discovery times of visited vertices
    // parent[] --> Stores parent vertices in DFS tree
    bridgeUtil(u,visited,disc,low,parent)
    {
        // Mark the current node as visited
        visited[u] = true;

        // Initialize discovery time and low value
        disc[u] = low[u] = ++this.time;

        // Go through all vertices adjacent to this

        for(let i of this.adj[u])
        {
            let v = i;  // v is current adjacent of u

            // If v is not visited yet, then make it a child
            // of u in DFS tree and recur for it.
            // If v is not visited yet, then recur for it
            if (!visited[v])
            {
                parent[v] = u;
                this.bridgeUtil(v, visited, disc, low, parent);

                // Check if the subtree rooted with v has a
                // connection to one of the ancestors of u
                low[u]  = Math.min(low[u], low[v]);

                // If the lowest vertex reachable from subtree
                // under v is below u in DFS tree, then u-v is
                // a bridge
                if (low[v] > disc[u])
                    document.write(u+" "+v+"<br>");
            }

            // Update low value of u for parent function calls.
            else if (v != parent[u])
                low[u]  = Math.min(low[u], disc[v]);
        }
    }

    // DFS based function to find all bridges. It uses recursive
    // function bridgeUtil()
    bridge()
    {
        // Mark all the vertices as not visited
        let visited = new Array(this.V);
        let disc = new Array(this.V);
        let low = new Array(this.V);
        let parent = new Array(this.V);


        // Initialize parent and visited, and ap(articulation point)
        // arrays
        for (let i = 0; i < this.V; i++)
        {
            parent[i] = this.NIL;
            visited[i] = false;
        }

        // Call the recursive helper function to find Bridges
        // in DFS tree rooted with vertex 'i'
        for (let i = 0; i < this.V; i++)
            if (visited[i] == false)
                this.bridgeUtil(i, visited, disc, low, parent);
    }
}

// Create graphs given in above diagrams
document.write("Bridges in first graph <br>");
let g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
document.write("<br>");

document.write("Bridges in Second graph<br>");
let g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.bridge();
document.write("<br>");

document.write("Bridges in Third graph <br>");
let g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.bridge();

// This code is contributed by avanitrachhadiya2155
</script>

Output

Bridges in first graph 
3 4
0 3

Bridges in second graph 
2 3
1 2
0 1

Bridges in third graph 
1 6

Time Complexity: O(V+E), 

• The above approach uses simple DFS along with Tarjan’s Algorithm. 
• So time complexity is the same as DFS which is O(V+E) for adjacency list representation of the graph.

Auxiliary Space: O(V) is used for visited, disc and low arrays.